Etude de fonctions numériques (4)
1.3 Eléments de symétrie d'une courbe
1.3.1 La parité
Soit f est une fonction et (C) sa courbe représentative dans un repère orthonormé (O;i→;j→).
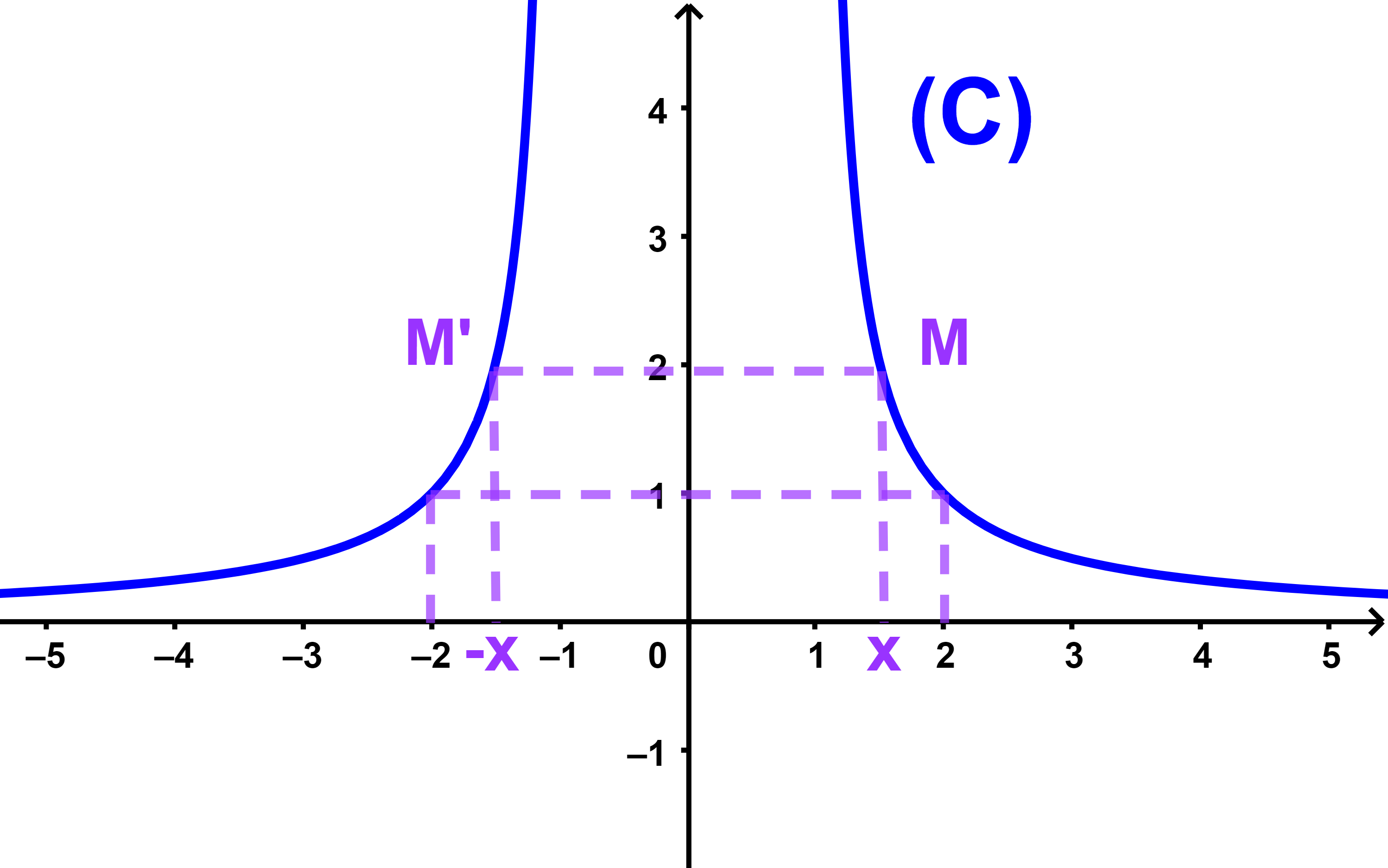
1) Si f est paire alors sa courbe
(C) est symétrique par rapport à l'axe des ordonnées.
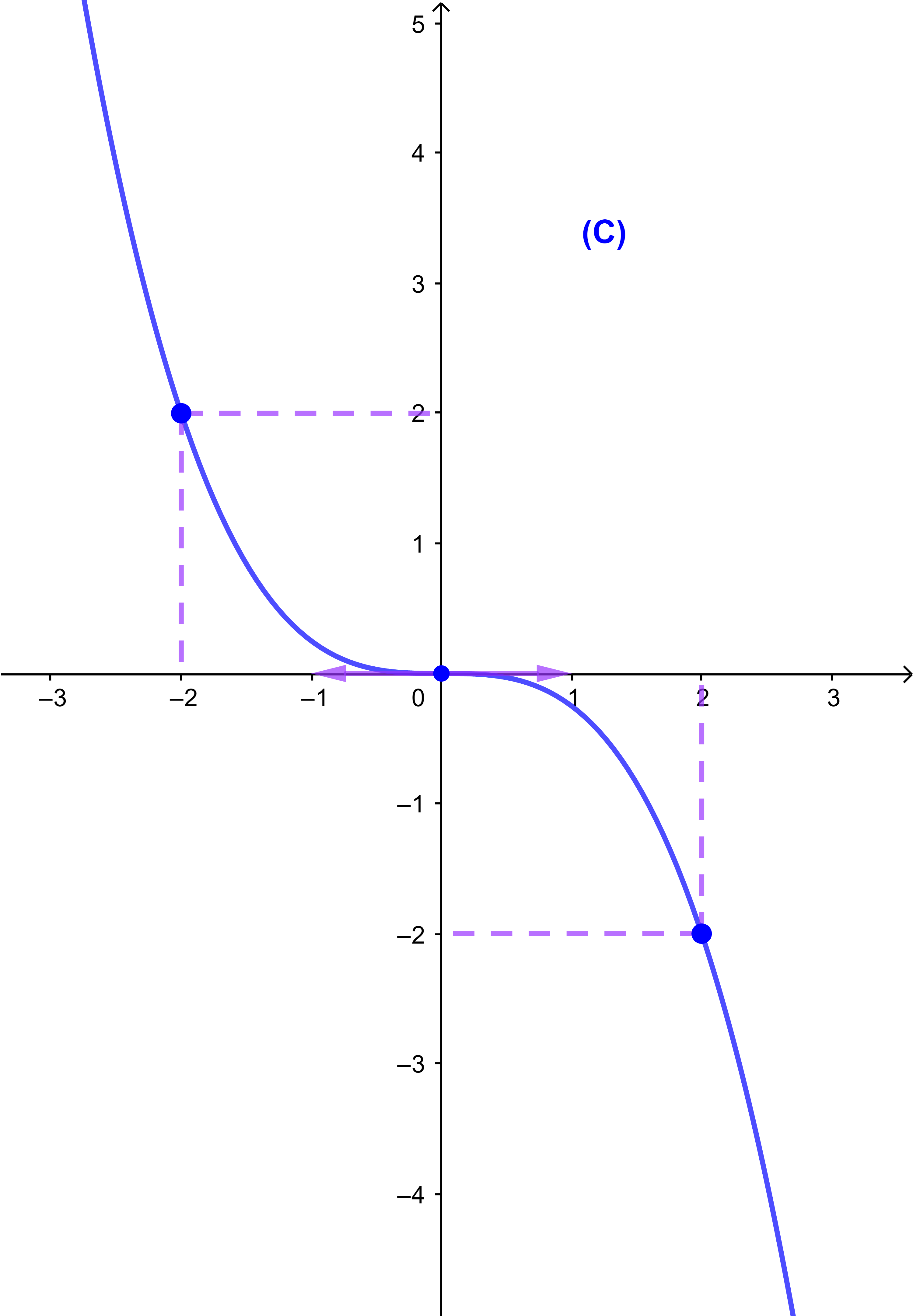
2) Si f est une fonction impaire alors sa courbe
(C) est symétrique par rapport à l'origine du repère.
f est paire
f est impaire
1.3.2 la périodicité
Rappel
Une fonction f est périodique de période T si
1) (∀x∈D): x+T∈D et x-T∈D
2) (∀x∈D): f(x+T)=f(x)
Propriété
Si f est une fonction périodique de période T,
il suffit de tracer la courbe (C) sur un intervalle d'amplitide T
et compléter la courbe en utilisant la translation du vecteur
u→=Ti→.
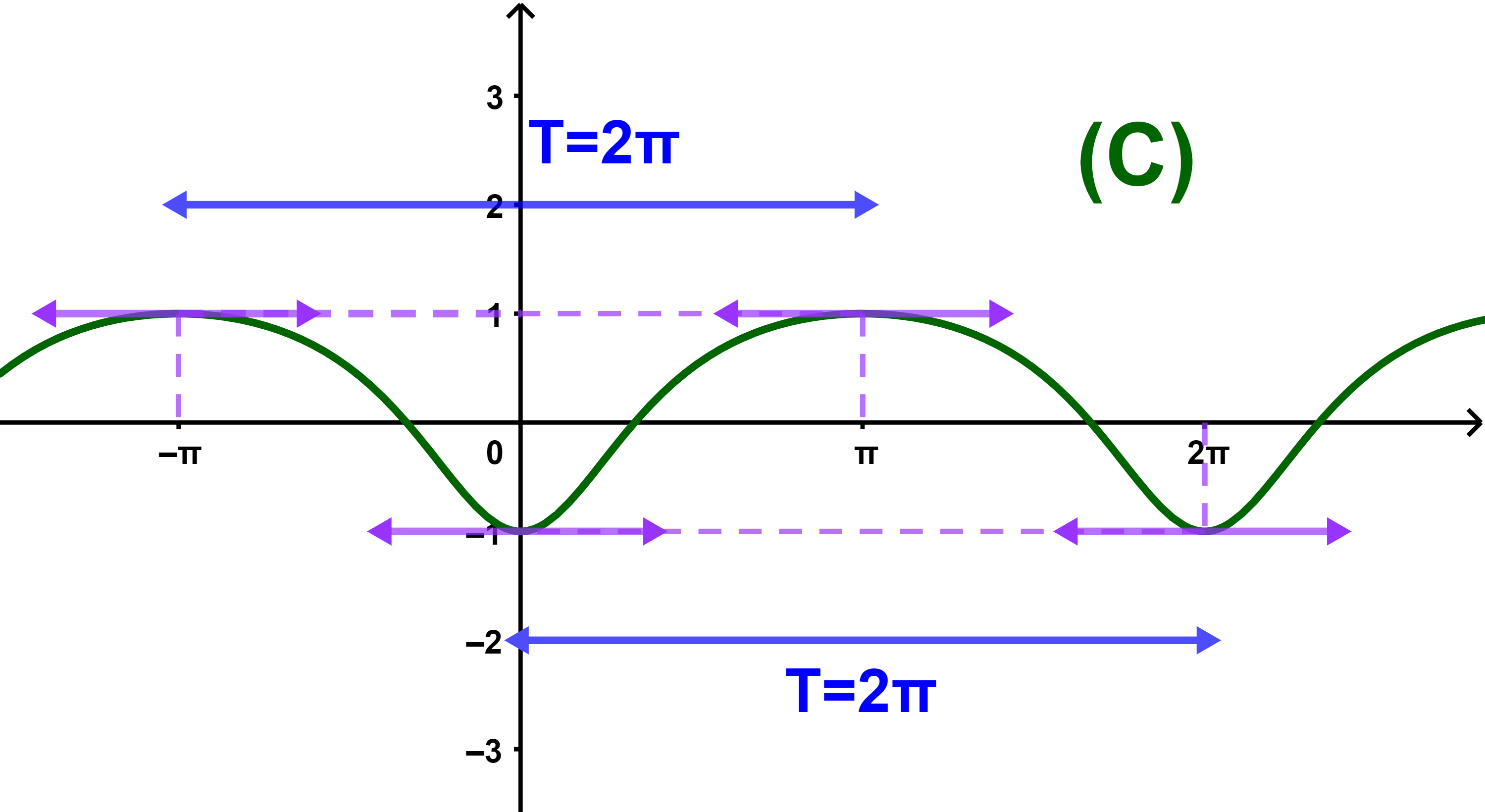
Exemples
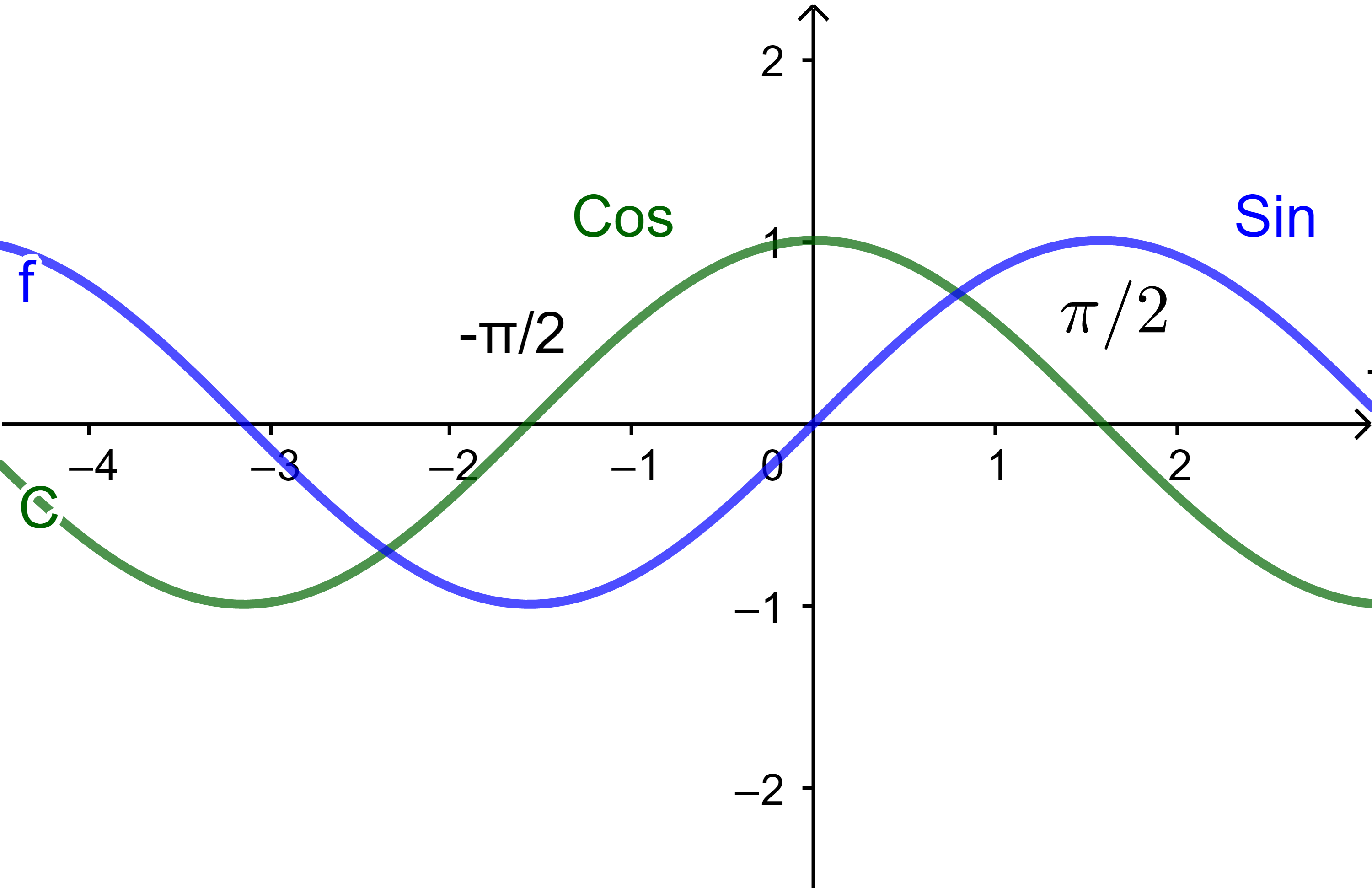
Les fonctions cos et sin sont périodiques de période 2π,
il suffit d'étudier ces fonctions sur un intervalle d'amplitude 2π
Exemples: [-π;π] ou [0;2π] ;...
1.3.3 Axe de symétrie
Propriété : Soit f une fonction numérique
et (C) sa courbe représentative.
La droite (D) d'équation x=a est un axe de symétrie de (C)
si (∀x∈Df): 2a-x∈Df et f(2a-x)=f(x).
1.3.4 Centre de symétrie
Propriété
f est une fonction numérique de variable x ; Df son ensemble de définition et (C) sa courbe représentative dans un repère(O;i→;j→).
Le point A(a;b) est un centre de symétrie de (C)
si (∀x∈Df): 2a-x∈Df et
f(2a-x)=2b-f(x).
Exemple Soit f une fonction définie par
| f(x) = | x²-2x+2 |
| x-1 |
Montrer que W(1;0) est un centre de symétrie de (C).
Correction
D={x∈IR/ x-1≠0}=IR\{1}.
Soit x∈D montrons que 2.1-x∈D
2-x=1⇔-x=1-2=-1⇔x=1
et puisque x≠1 alors (2-x)∈D.
| f(2-x) = | (2-x)²-2(2-x)+2 |
| 2-x-1 | |
| = | x²-2x+2 |
| -(x-1) |
donc f(2-x)=-f(x)=2.0-f(x) ainsi le point W(1;0) est un centre de symétrie de la courbe (C).