Dérivation et représentation (15)
Exercice 1 tp
Soit f une fonction numérique f définie par
f(x) = √(x²-4x+3)
et (C) sa courbe représentative dans un repère
orthonormé (O ; i→ ; j→)
1) Montrer que x²-4x+3=(x-1)(x-3) et déduire D le domaine de définition de f
2) Calculer les limites suivantes
lim -∞ | f(x) | lim +∞ | f(x) |
3) (a) Etudier la dérivabilité de f en 1 et en 3
Et déduire que (C) admet deux demi-tangentes
(b) Montrer que ∀x∈D\{1;3}
| f '(x) = | x-2 |
| f(x) |
et tracer le tableau de variations de f
4) Tracer la courbe (C)
5) Soit g la restriction de f sur l'intervalle
I=]-∞ ; 1[
(a) Montrer que g admet une fonction réciproque définie sur J qui doit être déterminé
(b) Calculer f(-1)
(c) Montrer que la fonction g-1 est dérivable au point 2√(2)
et déterminer (g-1)'(2√(2))
(d) Déterminer les variations de g-1 sur J
Correction
1) (x-1)(x-3) = x²-3x-x+3 = x²-4x+3
Donc x²-4x+3=(x-1)(x-3)
x∈D ⇔ x²-4x+3 ≥ 0 ⇔ (x-1)(x-3) ≥0
| x | -∞ | 1 | 3 | +∞ | |||
| x²-4x+3 | + | 0 | - | 0 | + |
Donc D=]-∞;1]∪[3;+∞[
2) Limite en -∞
lim -∞ | x²-4x+3 | = | lim -∞ | x² = +∞ |
| Donc | lim -∞ | f(x) = +∞ |
Limite en +∞
lim +∞ | x²-4x+3 | = | lim +∞ | x² = +∞ |
| Donc | lim +∞ | f(x) = +∞ |
3) (a) Dérivabilité de f en 1- on a f(1)=0
x-1 ≤0 donc x-1 =-|x-1| = -√(x-1)²
lim 1- |
f (x)-f(1) | = | lim 1- |
√(x²-4x+3) |
| x-1 | -√(x-1)² |
| = | lim 1- |
- √( | (x-1)(x-3) | ) |
| (x-1)² |
| = | lim 1- | - √( | x-3 | ) |
| x-1 |
| On a | lim 1- |
x-3 | = | -1 |
| x-1 | 0- |
| Donc | lim 1- |
√( | x-3 | )=+∞ |
| x-1 |
| Ainsi | lim 1- | f (x)-f(1) | = - ∞ |
| x-1 |
Alors f n'est pas dérivable au point 1
Et de plus la courbe (C) admet une demi-tangente verticale au point d'abscisse 1
Dérivabilité de f en 3+ , f(3)=0
x-3 ≥0 donc x-3 =|x-3| = √(x-3)²
lim 3+ | f (x)-f(3) | = | lim 3+ | √(x²-4x+3) |
| x-3 | √(x-3)² |
| = | lim 3+ | √( | (x-1)(x-3) | ) |
| (x-3)² |
| = | lim 3+ | √( | x-1 | ) |
| x-3 |
| On a | lim 3+ |
x-1 | = | 2 |
| x-3 | 0+ |
| Donc | lim 3+ |
√( | x-1 | )=+∞ |
| x-3 |
| Ainsi | lim 3+ | f (x)-f(3) | = + ∞ |
| x-3 |
Alors f n'est pas dérivable au point 3
Et de plus la courbe (C) admet une demi-tangente verticale au point d'abscisse 3
(b) Le polynôme p(x)=x²-4x+3 est strictement positif et dérivable sur D\{1;3} donc f est dérivable sur D\{1;3} .
Soit x∈D\{1;3}
| f '(x) = | (x²-4x+3)' | = | 2x-4 |
| 2√(x²-4x+3) | 2√(x²-4x+3) | ||
| = | 2(x-2) | = | x-2 |
| 2√(x²-4x+3) | √(x²-4x+3) |
| Ainsi | f '(x) = | x-2 |
| f(x) |
Signe de f '(x)
f'(x)=0 ⇔ x-2= 0⇔ x=0
f'(x) > 0 ⇔ x > 2
donc f est strictement croissante
sur I=[2 ; +∞[∩D = [3;+∞[ car [2;3[⊄D
f'(x) < 0 ⇔ x < 2
donc f est strictement décroissante
sur J=]-∞ ; 2[∩D = ]-∞ ; 1] car ]1 ; 2]⊄D
| x | -∞ | 1 | 3 | +∞ | |||
| f' (x) | - | 0 | 0 | + | |||
| f | +∞ | ↘ |
0 | 0 |
↗ |
+∞ |
4) La courbe (C)
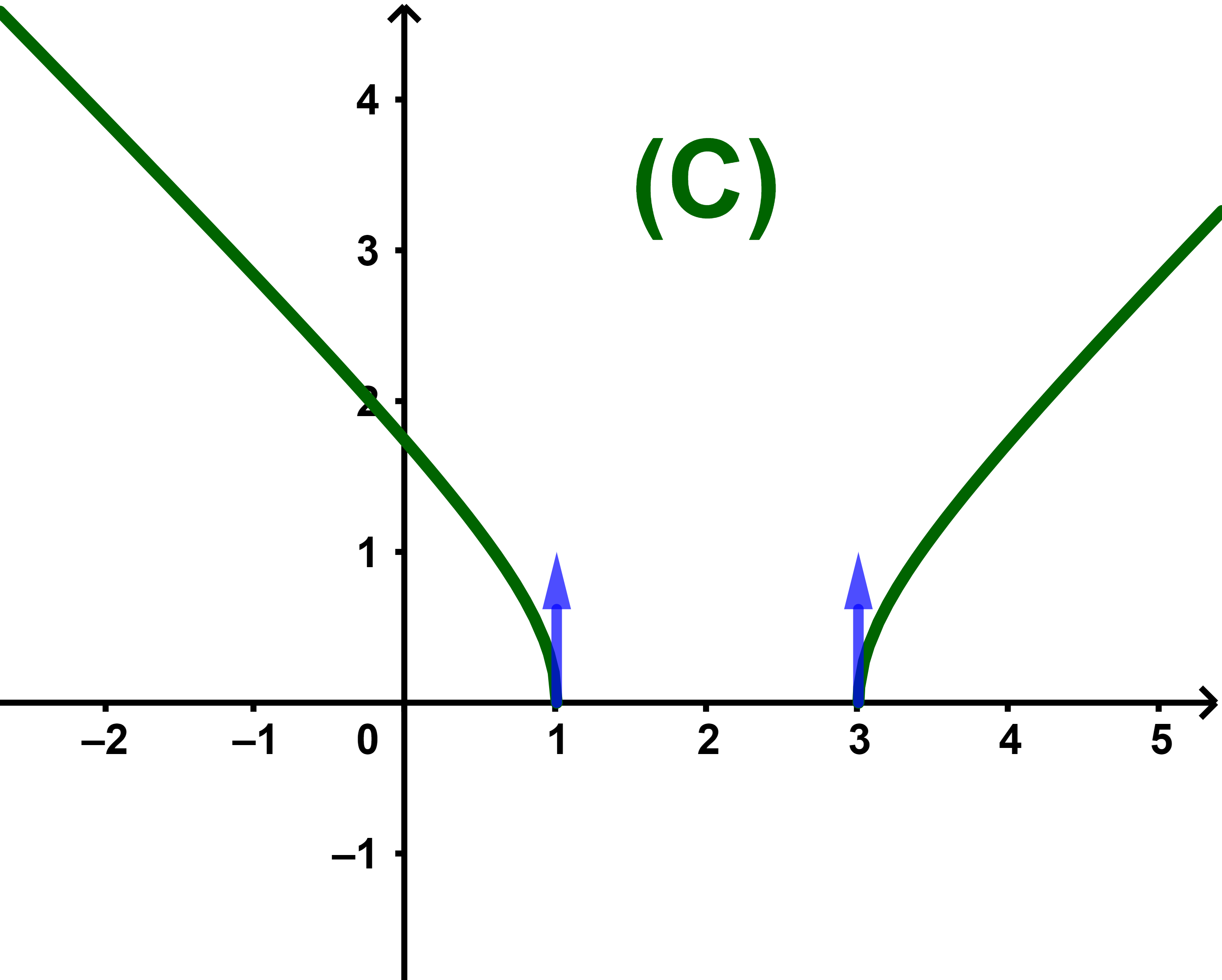
5) (a) f est continue sur D en particulier
sur I=]-∞ ; 1] donc sa restriction g est continue sur I
Et on a f est strictement décroissante sur I
Donc g est strictement décroissante sur I
Ainsi g admet une fonction réciproque
définie de J=f(I) = f(]-∞ ; 1]) vers I
| J = [f(1) ; | lim -∞ | f(x)[ |
Donc J = [0 ; +∞[
(b) f(-1) = √((-1)²-4(-1)+3) = 2√(2)
(c) On a f(-1)=2√(2) et 2√(2)∈J
donc g-1(2√(2)) = -1
Puisque g est dérivable au point -1
et g '(-1) = (-3√2)4-1 ≠ 0
alors g-1 est dérivable au point 2√(2)
Et on a
| (g-1)'(2√(2)) = | 1 | = | -4 |
| g '(-1) | 3√(2) |
| Donc | (g-1)'(2√(2)) = | -2√(2) |
| 3 |
(d) La fonction g est strictement décroissante sur I donc sa fonction réciproque est également strictement décroissante sur J