Dérivation et représentation (3)
Exercice 1 tp
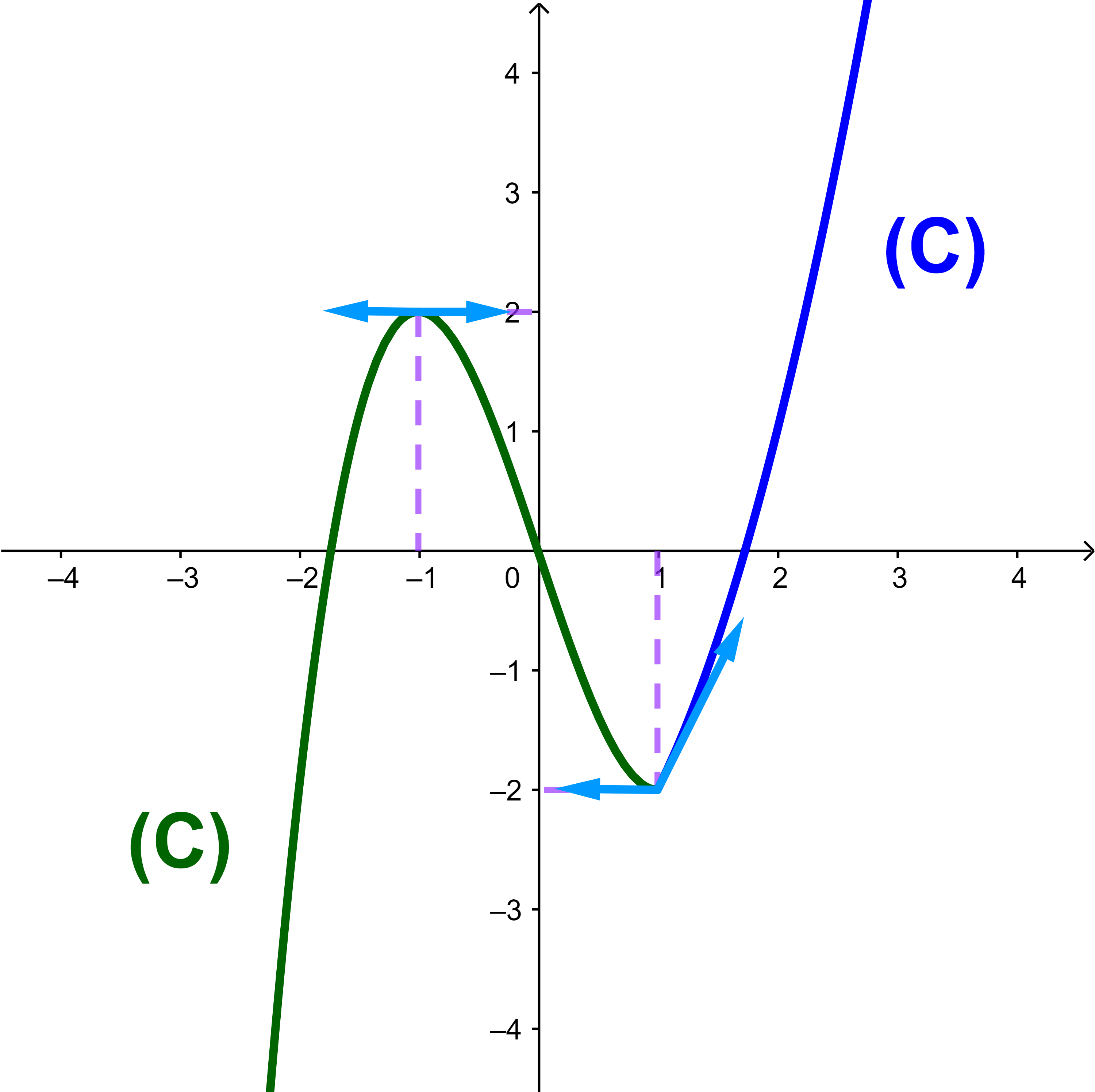
Soit f une fonction définie par
| f(x)=x³-3x; x≤1 | |
| f(x)= x²-3 si x>1 |
1) Montrer qaue f n'est pas dérivable au point 1
et déterminer les équations des demi-tangentes au points A(1;f(1))
2) Déterminer l'équation de la tangente au point B(-1;f(-1))
Correction
On ne peut pas remplacer 1 dans l'expression f(x)=x²+3
car cette expression est valable pour les nombres supérieurs stricts à 1,
on a f(1)=1³-3.1=-2
lim 1+ |
f(x)-f(1) | = | lim 1+ |
x²-3+2 | x-1 | x-1 |
| = | lim 1+ |
x²-1 | lim 1+ |
(x+1) | = 2 | x-1 |
f est dérivable à droite à 1 et f 'd(1)=2
ainsi (C) admet une demi-tangente à droite au point A(1;-2)
d'équation y=2(x-1)-2 ou encore y = 2x-4
lim 1- |
f(x)-f(1) | = | lim 1- |
x³-3x+2 | x-1 | x-1 |
on pose p(x)= x³-3x+2
on a p(1)= 1-3+2=0 donc le polynome p(x) est divisble par x-1 ou encore il existe un polynome q(x) de degré 2 tel que
p(x)=(x-1)q(x)
| x³ | +0x² | -3x | +2 | x-1 | |
| -x³ | +x² | x²+x-2 | |||
| 0 | +x² | -3x | +2 | ||
| -x² | +x | ||||
| 0 | -2x | +2 | |||
| +2x | -2 | ||||
| 0 | 0 |
donc q(x)=x²+x-2
ainsi x³-3x+2 = (x-1)(x²+x-2)
lim 1- |
f(x)-f(1) | = | lim 1- |
(x-1)(x²+x-2) | x-1 | x-1 |
| = | lim 1- |
x²+x-2 | = 0 |
donc f est dérivable à gauche à 1 et f 'g(1)=0
ainsi (C) admet une demi-tangente à gauche à 1
d'équation y = 0(x-1)-2
ou encore y = -2 cette demi-tangente est parallèle à l'axe des abscisses
On a f 'g(1)≠f 'd(1) donc f n'est pas dérivable en 1
2) Equation de la tangente au point B(-1;f(-1)),
on étudie la dérivabilité de f au point -1
-1 < 1 donc on s'intéresse à l'expression
f(x)=x³-3x;
f(-1)=-1+3=2
lim -1 |
f(x)-f(-1) | = | lim -1 |
x³-3x-2 | x+1 | x+1 |
on pose h(x)=x³-3x-2, h(-1)=0 donc h(x) est divisible par x+1
| x³ | +0x² | -3x | -2 | x+1 | |
| -x³ | -x² | x²-x-2 | |||
| 0 | -x² | -3x | -2 | ||
| +x² | +x | ||||
| 0 | -2x | -2 | |||
| +2x | +2 | ||||
| 0 | 0 |
lim -1 |
f(x)-f(-1) | = | lim -1 |
x²-x-2 = 0 = f '(-1) | x+1 |
f '(-1) = 0 signifie que (C) admet une tangente horizontale d'équation y=f(-1)=2