4.2 Suite définie par l'integrale

4.2.1 Rappel

Le plan est rapporté à un repère orthonormé (O;i^→;j^→). On considère une fonction f continue et positive sur un intervalle [a;b] et (C) sa courbe représentative. L'intégrale I définie par

I =

b ∫ a

f(x)dx

représente S l'aire du domaine délimité par la courbe (C) ; l'axe des abscisses et les deux droites (D):x=a et (D'):x=b.

Nous avons déjà étudié la première façons au début de ce tutoriel pour tracer les rectangles de largeur δ et de hauteur f(x_i).
L'aire de chaque rectangle est égal à δ.f(x_i).

un = δ .	k=n-1 Σ k=0	f(a+kδ)

et on a (∀n∈IN)

un ≤

b ∫ a

f(x)dx

Nous continuons à étudier la deuxième façon
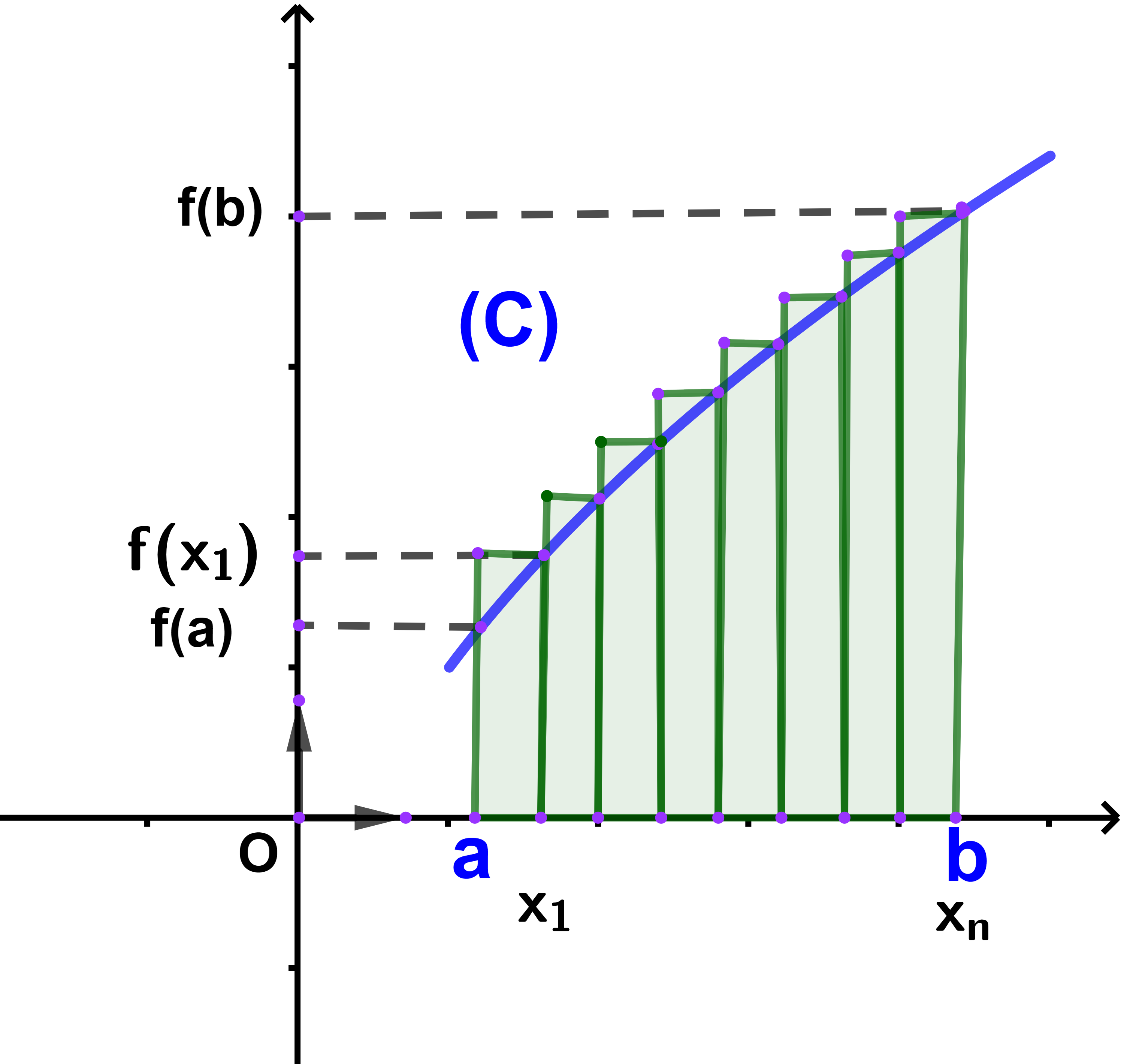
Deuxième façon : un des sommets de chaque rectangle est au-dessus de la courbe (C) alors la somme de leurs surfaces (est en excès) est notée v_n.
v_n = δ.f(x₁) + δ.f(x₂) + .. + δ.f(x_n)

vn = δ .	k=n Σ k=1	f(a+kδ)

Donc (∀n∈IN)

un ≤

b ∫ a

f(x)dx

≤ vn

et quand n→+∞ alors les deux suites (u_n) et (v_n)_n≥1 tendent vers S.

Remarque
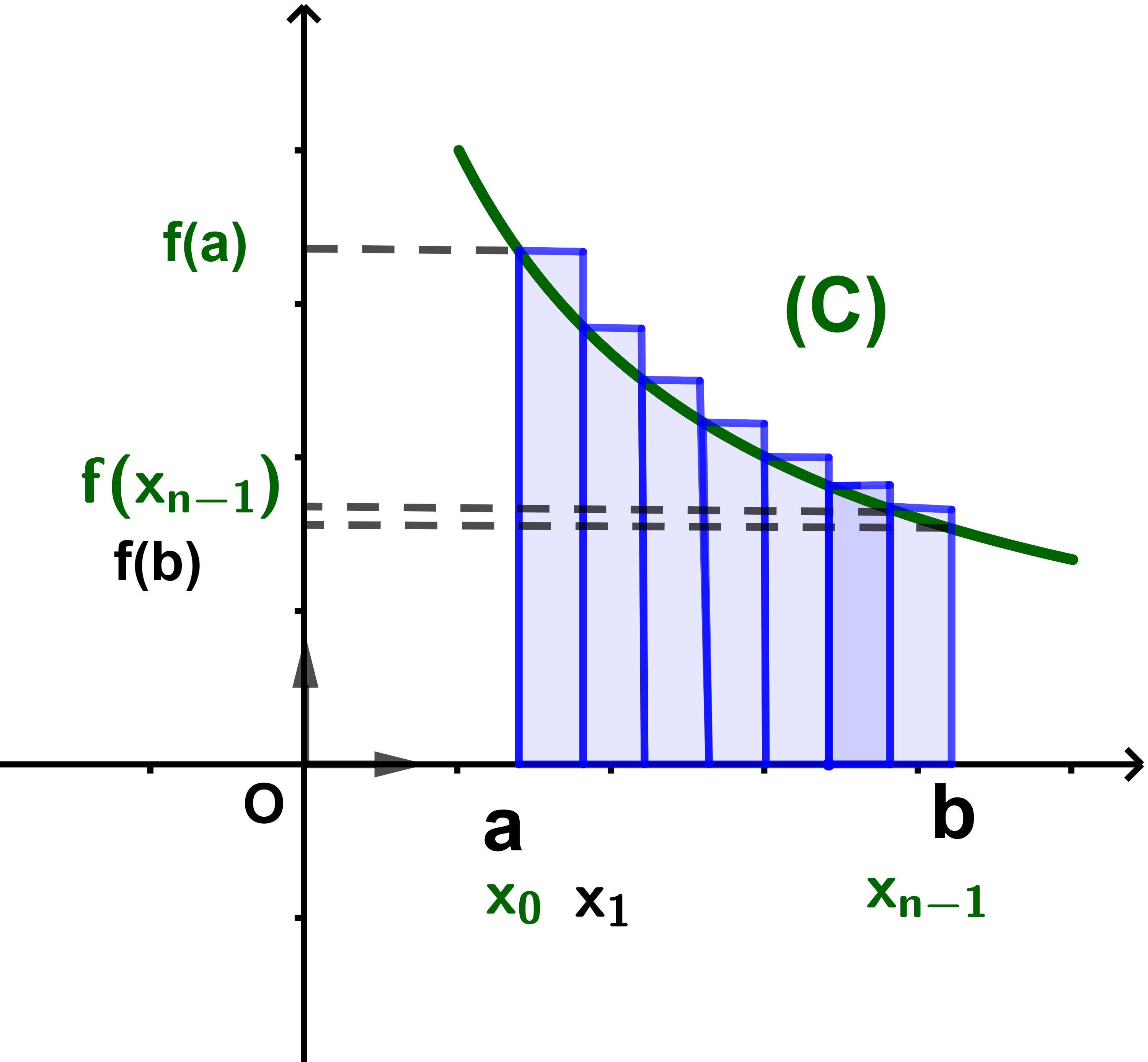
Si la fonction f est décroissante sur un intervalle I alors les deux suites (u_n) et (v_n)_n≥1:

un = δ .	k=n-1 Σ k=0	f(a+kδxi)
vn = δ .	k=n Σ k=1	f(a+kδxi)

donc

vn ≤

b ∫ a

f(x)dx

≤ un

Exemple
Soit f une fonction numérique définie par

f(x) =	8
	x+1

On considère l'intervalle I = [1,2;4,1].
f est continue sur I donc admet une integrale et puisque elle est positive donc l'aire du domaine délimité par la courbe (C) et les droites (D):x=1,2 et (D'):x=4,1 est définie par

S =

4,1 ∫ 1,2

f(x)dx

Donc

S = 8 . [ln(x+1)]

4,1 1,2

= 8(ln(5,1) - ln(2,2))

.UA

De plus la fonction f est décroissante sur I
donc les deux suites (u_n) et (v_n)_n≥1:

un	=	2,9	k=n-1 Σ k=0	f(1,2 + k.	2,9	)
		n			n

vn	=	2,9	k=n Σ k=1	f(1,2 + k.	2,9	)
		n			n

Vérifiant les inéquations suivantes

vn ≤

b ∫ a

f(x)dx

≤ un

ou encore v_n≤8(ln(5,1)-ln(2,2)).UA≤u_n.