Calcul Intégral (15)
Exercice 1 tp
Soit f une fonction numérique définie sur IR+ par
| f(x) = | ln(x²+2x+1) ∫ 0 |
1 | dt |
| 1 + et |
1) Déterminer D, l'ensemble de définition de f
2) Montrer que f est continue et dérivable sur IR+
3) Calculer f '(x) pour tout x∈D et déduire que f est strictement croissante sur D
4) Montrer que ∀x∈D
| f(x) = ln2( | x²+2x+1 | ) |
| x²+2x+2 |
5) (a) Calculer
lim +∞ | f(x) |
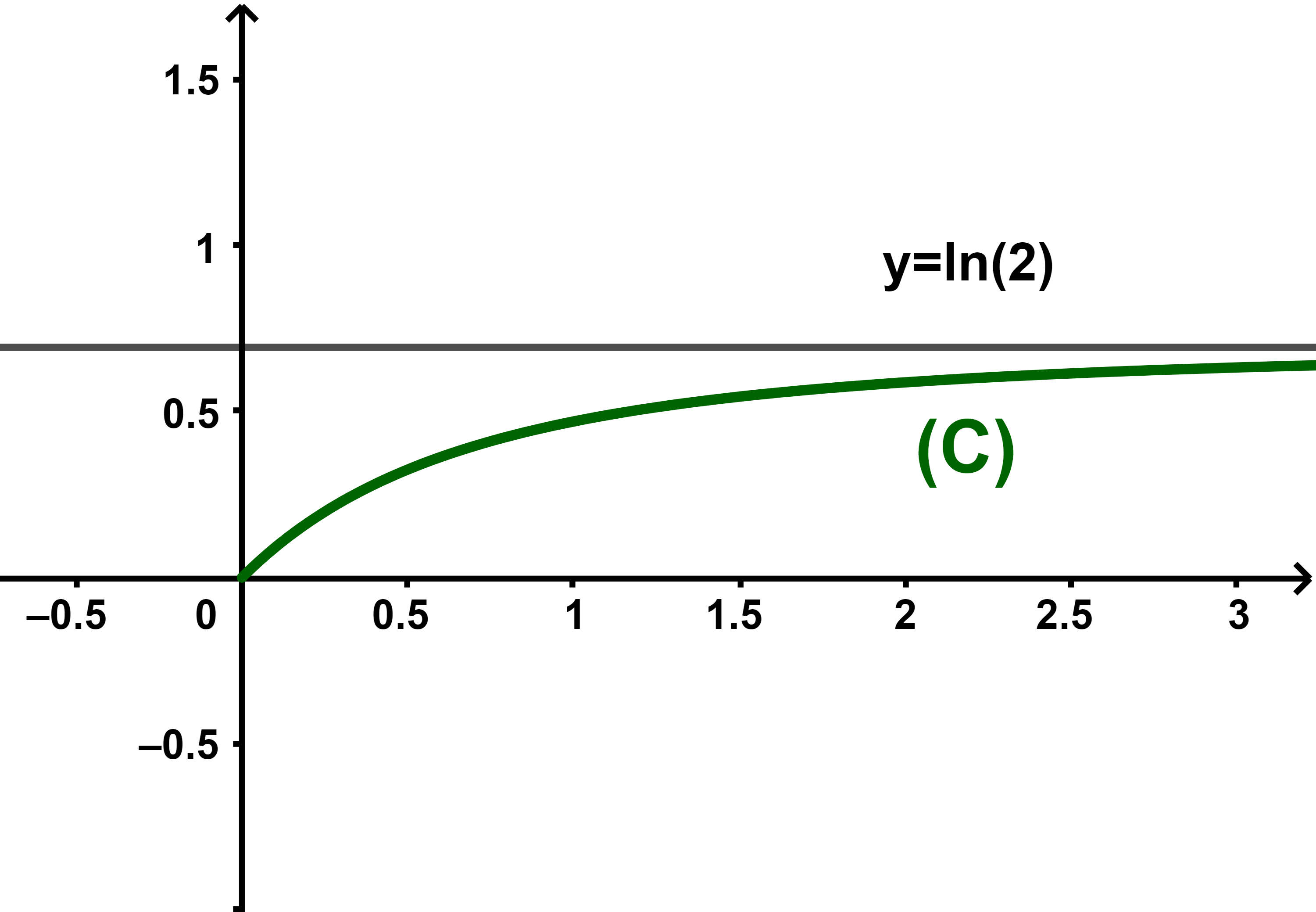
et déduire que (C) admet une asymptote au voisinage de +∞
(b) Dresser le tableau de variations de f
(c) Construire la courbe (C) dans un repère orthonormé
Correction
1) f est une fonction numérique définie par une integrale sous la forme
| f(x) = | φ(x) ∫ 0 | g(t) | dt |
ou φ(x) = ln(x²+2x+1)
| et g(t) = | 1 |
| 1 + et |
Premièrement on détermine le domaine de définition de φ
Dφ = {x∈IR+ / x²+2x+1 > 0}
= {x∈IR+ / (x+1)² > 0} ={x∈IR / x+1≠0}
Puisque ∀x∈IR+ on a x≠-1
Donc Dφ = IR+ .
Soit x∈IR+
La fonction g est définie et continue sur l'intervalle I = [0 ; φ(x)]
donc elle est intégrable sur cet intervalle
Donc la fonction f est bien définie sur IR+
Ainsi Df = IR+
2) On a dit précédement que g est est continue sur I donc elle admet des primitives sur cet intervalle
On choisit une , notée G
Donc ∀x∈IR+ on a f(x) = G(φ(x)) - G(0)
La fonction G est dérivabe sur IR+
| G'(x) = g(x) = | 1 |
| 1+ex |
La fonction φ est définie ; continue et dérivable sur IR+
Car φ est une composée de deux fonctions ln et p: x→x²+2x+1 où p est strictement positive et dérivable sur IR+
| φ(IR+)=[φ(0) ; | lim +∞ | φ(x) [ |
Ou encore φ(IR+)=[0 ; +∞[⊂IR+ donc la composée Goφ est définie ; continue et dérivable sur IR+
Ainsi f est continue et dérivable sur IR+
3) On a ∀x∈IR+
f '(x)= G'(φ(x)).φ'(x)
Puisque ∀x∈IR+
| φ'(x) = | 2x+2 | = | 2 |
| (x+1)² | x+1 |
Alors
| f '(x) = | 2 |
| (x+1)(1+eφ(x)) |
| = | 2 |
| (x+1)(1+x²+2x+1) |
Et par conséquent ∀x∈IR+
| f '(x) = | 2 |
| (x+1)(x²+2x+2) |
Variations de f
∀x∈IR+ on a x²+2x+2 > 0 et x+1 > 0
donc f ' est strictement positive sur IR+
Et donc f est strictement croissante sur IR+
4) Soit x∈IR+ et t∈[0 ; ln(x²+2x+1)] on a
| 1 | = 1 - | et |
| 1+et | 1+et |
Donc
| f(x) = | [t - ln(1+et)] | ln(x²+2x+1) 0 |
Ou encore
| = | ln(x²+2x+1) | - ln(1+x²+2x+1) + ln(2) |
Et par suite ∀x∈IR+
| f(x) = ln2( | x²+2x+1 | ) |
| x²+2x+2 |
5) (a) On a
lim +∞ |
f(x) = | lim +∞ |
ln | 2(x²+2x+1) |
| x²+2x+2 |
Puisque
lim +∞ |
2(x²+2x+1) | = | lim +∞ |
2x² |
| x²+2x+2 | x² |
| Alors | lim +∞ |
ln | 2(x²+2x+1) | = ln(2) |
| x²+2x+2 |
| Ainsi | lim +∞ | f(x) = ln(2) |
Et cela signifie que (C) admet une asymptote au voisinage de +∞
(b) Tableau de variations de f
| x | 0 | +∞ | ||
| f'(x) | + | |||
| f | 0 | ↗ |
ln(2) |
(c) L acourbe (C)