Exercice 1 tp

Soit f une fonction numérique définie sur IR par

f(x) =

x ∫ 0

(2t)et²-1

dt

1) Etudier la parité de la fonction f
2) Montrer que ∀x∈IR⁺

f(x) ≥	1	x4 - x²
	2

Et calculer

lim +∞

f(x)

3) Montrer que f est continue et dérivable sur IR
4) Calculer f '(x) pour tout x∈IR et déterminer les variations de f
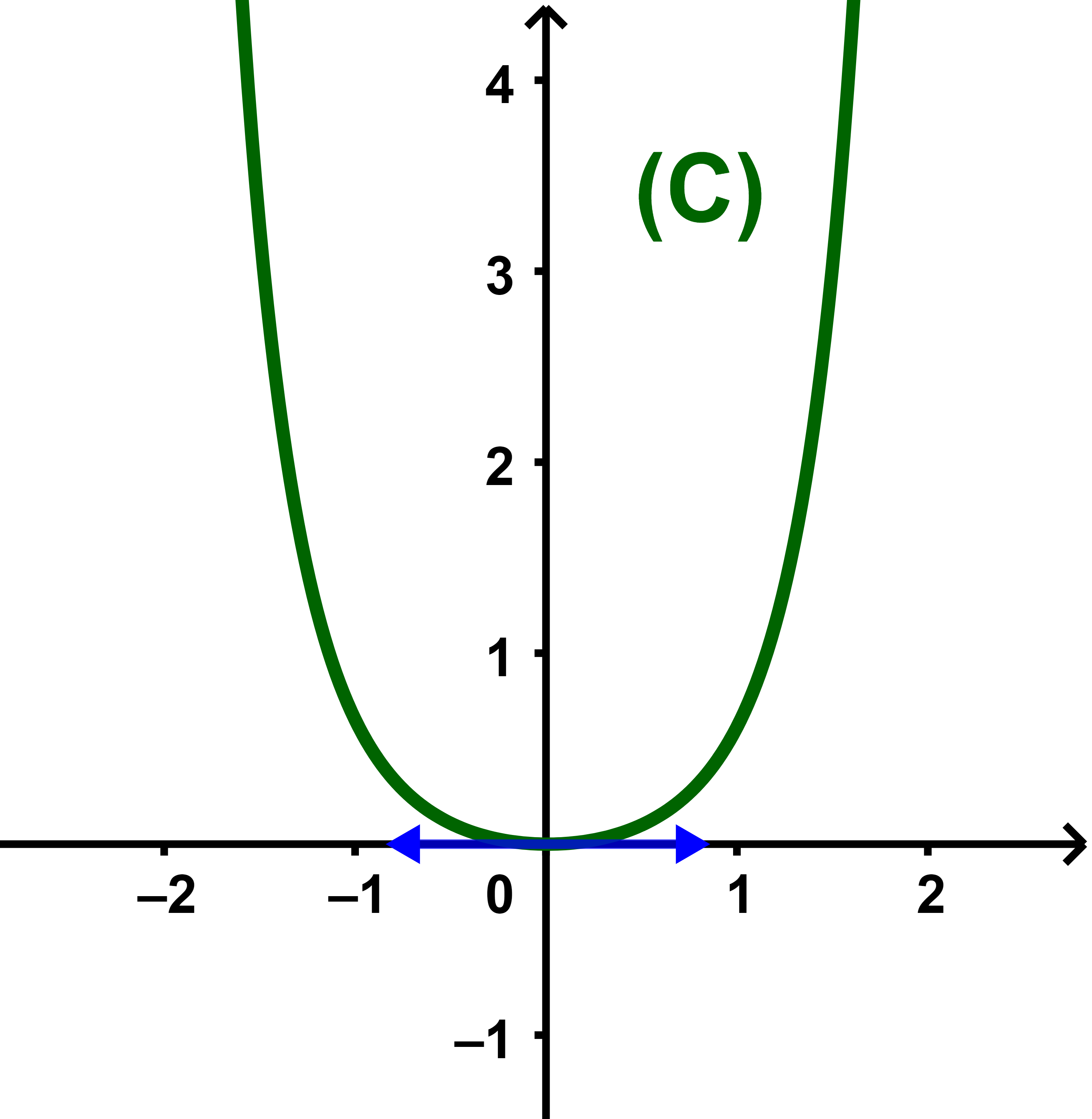
5) Tracer la courbe (C) dans un repère orthonormé

Correction

1) Soit g la fonction définie sur IR par
g(t) = (2t)e^t²-1
Soit x∈IR , g est le produit de deux fonctions continues sur I=[0 ; x] donc g est continue sur I et par suite elle admet une integrale sur I
Et donc la fonction f est définie sur IR
D = IR donc ∀x∈IR on a (-x)∈IR
Soit x∈IR

f(- x) =

- x ∫ 0

(2t)et²-1

dt

On pose t= - u donc dt = -du
si t=0⇒ u = 0 et si t=-x⇒ u = x

f(- x) =	x ∫ 0	(-2u)e(-u)²-1	(-1)du
=	x ∫ 0	(2u)eu²-1	du

Notons que l'integrale ne dépend pas du choix de la lettre u
Et donc f(-x) = f(x) et cela signifie que f est une fonction paire

2) On a ∀x∈IR, e^x ≥ x donc ∀t∈IR⁺ on a e^t²-1 ≥ t²-1
ou encore 2t.e^t²-1 ≥ 2t(t²-1)
Ou encore

f(x) ≥	1	[(t²-1)²]	x 0
	2
⇒ f(x) ≥	1	((x²-1)² - 1)
	2

Ainsi (∀x∈IR⁺)

f(x) ≥	1	x4 - x²
	2

Puisque

lim +∞	1	x4 - x²	=	lim +∞	1	x4 = +∞
	2				2

alors en utilisant le critère de convergence

On obtient

lim +∞

f(x) = +∞

3) Comme on a dit au dessus que g est continue sur I donc elle admet une primitive sur cet intervalle , notée G qui s'annule en 0 Donc ∀x∈IR on a f(x) = G(x)
La fonction G est continue et dérivable sur IR donc f est continue et dérivable sur IR

Soit x∈IR on a f '(x) = G '(x) = g(x)
Ainsi ∀x∈IR on a f '(x) = 2xe^x²-1
Variations de f, soit x∈IR
f'(x)=0 ⇔ 2xe^x²-1 = 0
⇔ x=0
Si x>0 alors f '(x) > 0 ainsi f est strictement croissante sur IR⁺

f est une fonction paire donc f est strictement décroissante sur IR^-

x		-∞		0		+∞
f '(x)		+∞	↘	0	↗	+∞

Déterminons G , la fonction x→x²-1 est dérivable sur IR et (x²-1)'=2x
Donc f '(x)=(x²-1)'e^x²-1 =(e^x²-1)'
Et donc G(x)=e^x²-1+k
et G(0)=0 donc k=-e^-1
Ainsi ∀x∈IR on a f(x)=G(x)=e^x²-1-e^-1