Théorème de Rolle et théorème des accroissements finis (1)
1- Théorème de Rolle
1.1 Théorème
Soit f une fonction définie sur un intervalle [a;b].
Si f vérifie les trois conditions suivantes
(1) f est continue sur le segment [a;b]
(2) f est dérivable sur l'intervalle ouvert ]a;b[
(3) f(a) = f(b)
alors il existe c∈]a;b[ tel que f'(c)=0.
1.2 Exemples
1.2.1 Exemple 1
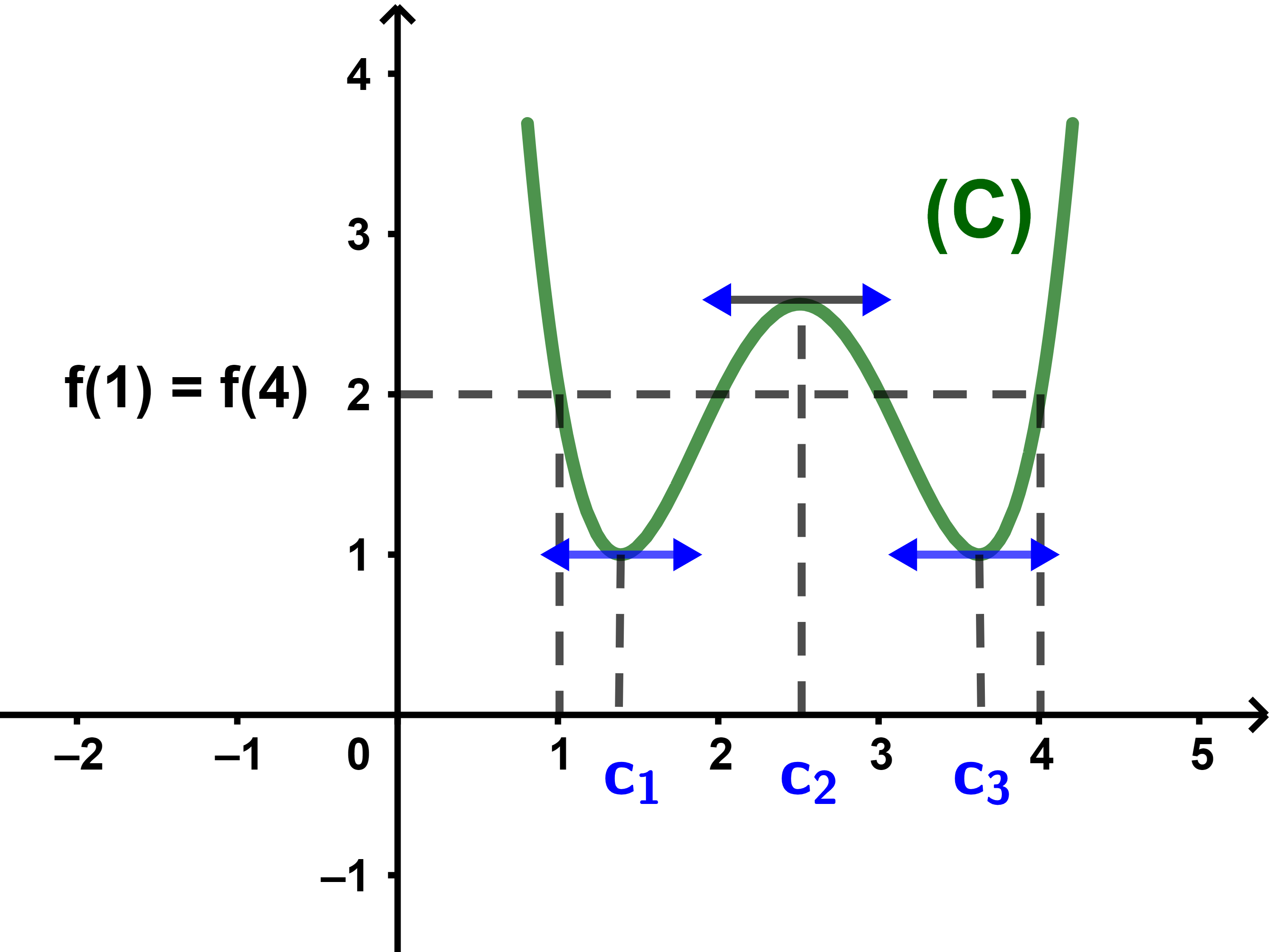
Est ce que la fonction f définie sur l'intervalle
I = [1 ; 4] par
f(x) = 2+(x-1)(x-2)(x-3)(x-4) vérifie les condtions du théorème de Rolle ?
Correction
1) f est une restriction d'un polynôme donc continue sur l'intervalle I.
2) f est une restriction d'un polynôme donc dérivable sur I en particulier sur ]1 ; 4[.
3) f(1) = 2 et f(4) = 2.
Donc f(1) = f(4)
ainsi la fonction f vérifie les conditions du théorème de Rolle.
(∃c∈]1 ; 4[): f'(c)=0.
1.2.2 Exemple 2
Est ce que la fonction f définie sur l'intervalle
I=[-√(3);√(3)] par
f(x) = x³ - 3x vérifie les condtions du théorème de Rolle ?
Correction
(1) f est une restriction d'un polynôme donc continue sur I.
(2) f est une restriction d'un polynôme donc dérivable sur I
en particulier sur ]-√(3);√(3)[.
(3) f(-√(3))=-3√(3) - (3(-√(3))=0
et f(√(3))= 3√(3) - 3√(3)=0
donc f(-√(3)) = f(√(3))
ainsi f vérifie les conditions du théorème de Rolle.
(∃c∈]-√(3) ; √(3)[): f'(c)=0.
Vérification On a f'(x) = 3x²-3
f'(x)=0 ⇔ 3(x-1)(x+1)=0 ⇔ x=-1 ou x=1
-1;1∈]-√(3);√(3)[ et f'(-1)=0 et f'(1)=0
donc c existe dans l'intervalle ouvert
]-√(3);√(3)[.
2- Théorème des accroissements finis (TAF)
2.1 Théorème
Soit f une fonction définie sur un intervalle [a;b].
Si f vérifie les deux conditions suivantes
(1) f est continue sur le segment [a;b]
(2) f est dérivable sur l'intervalle ouvert ]a;b[
alors ∃c∈]a;b[: f(b)-f(a)=f'(c)(b-a).
Démonstration
| On pose k = | f(b)-f(a) |
| b-a |
et on considère une fonction φ définie sur I par
φ(x) = f(x)-k(x-a)
φ(a) = f(a) et φ(b) = f(a) donc φ(a) = φ(b)
φ est continue sur [a;b] et dérivable sur ]a;b[.
En utilisant le théorème de Rolle on déduit donc
(∃c∈]a;b[): φ'(c)=0.
Puisque
| φ'(x) = | f'(x) - k | = f '(x) - | f(b)-f(a) |
| b-a |
| alors f '(c) - | f(b)-f(a) | = 0 |
| b-a |
et donc ∃c∈]a;b[
| f '(c) = | f(b)-f(a) |
| b-a |
ainsi (∃c∈]a;b[): f(b)-f(a)=f'(c)(b-a).