المرجح في المستوى (1)
تمرين 1 tp
لتكن A; B و C ثلاث نقط بحيث
3AC→=4BC→
1) بين ان A مرجح النقطتين المتزنتين
(B;4) ; (C;-1)
2) لتكن D نقطة بحيث
2AC→+4BD→=O→
بين ان A مركز ثقل B; D
تصحيح
1) حسب علاقة شال
3AC→=4BC→⇔3AC→=4(AC→-AB→)
⇔ 4AB→+3AC→-4AC→=O→
⇔4AB→-AC→=O→
اذن A مرجح النقطتين المتزنتين
(B;4) ; (C;-1)
2) لدينا
2AC→+4BD→=O→
⇔2AC→+4(BA→+AD→)=0→
⇔2AC→-4AB→+4AD→
=O→
⇔8AB→-4AB→+4AD→
=O→
⇔4AB→+4AD→=0→
⇔AB→+AD→=0→
( لان
AC→=4AB→
اي
2AC→=8AB→)
اذن A مرجح (B;1);(D;1)
وهذا يعني A مركز ثقل B; D
تمرين 2 tp
G مرجح (A;k) و (B;t) حدد k و t في كل من الحالتين التاليتين
1) GA→ + GB→ = 2AB→
2) 2GA→ + AB→ = O→
تصحيح
G مرجح (A;k) و (B;t) يعني kGA→ + tGB→ = O→
1) GA→ + GB→ = 2AB→
⇔GA→ + GB→ = 2(AG→+GB→)
⇔3GA→ - GB→ = O→
وهذا يعني ان G مرجح النقطتين المتزنين (A;3) و (B;-1)
اذن k=3 ; t=-1
2) 2GA→ + AB→ = O→
⇔2GA→ + (AG→+GB→) = O→
⇔GA→ + GB→ = O→
وهذا يعني ان G مرجح النقطتين المتزنتين (A;1) و (B;1)
اذن k=1 ; t=1.
تمرين 3 tp
ليكن (ABC) مثلثا
و D نقطة بحيث AD→ = 1,5AB→
1) تحقق ان A مرجح (B;3) و (D;-2)
2) انشئ G مرجح (C;3) و (D;-2)
3) بين ان
DG→ = 3DC→
ثم استنتج ان AG→ و BC→ مستقيميتان
4) حدد مجموعة النقط M من المستوى بحيث
||-2MD→+3MB→||=||-2MD→+3MC→||
تمرين 4 tp
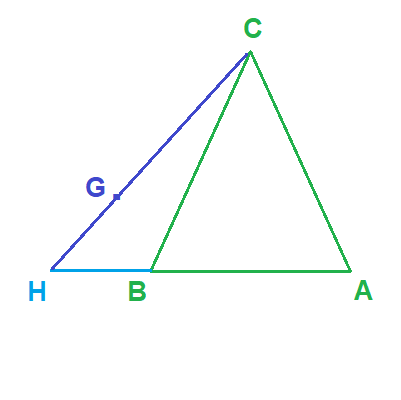
انشئ G مرجح (A;-1) ; (B;3) ; (C;1)
تصحيح
نلاحظ ان النقطتين (A,-1) ; (C,1) ليس لهما مرجحا لان
-1+1=0 اذن لا يمكن تطبيق التجميعية على A و C
نأخذ النقطتين (A;-1) ; (B;3) لان
-1+3=2≠0
اذن يقبلان مرجحا نرمز له ب H ومنه فان G مرجح النقطتين (H;2) ; (C;1)
يمكن ان نطبق التجميعية ايضا على النقطتين B; C لان
3+1=4≠0
ملاحظة يمكن رسم المرجح G برسم كل من H و C
لدينا H مرجح ل (A;-1) ; (b;3) يعني
∀M: -MA→+3MB→=(-1+3)MH→
⇔
∀M: -MA→+3MB→=2MH→
⇔
-BA→=2BH→
يعني ان
| BH→ = - | 1 | BA→ |
| 2 |
ونعلم ان
∀M: -MA→+3MB→+MC→=3MG→
⇔
2MH→+MC→=3MG→
⇔
HC→=3HG→
وبالتالي
| HG→ = | 1 | HC→ |
| 3 |