المرجح في المستوي (2)
تمرين 5 tp
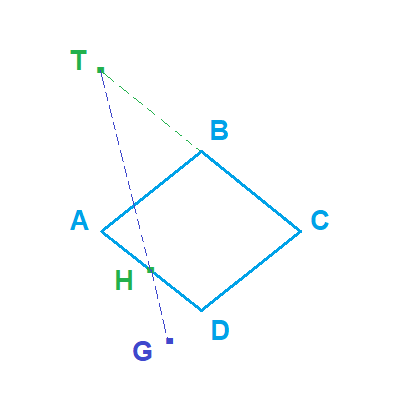
انشئ G مرجح (A;2) ; (B;-2) ; (C;1) و (D;2).
تصحيح
نلاحظ ان النقطتين (A,2) ; (B,-2) ليس لهما مرجحا لان
2+(-2)=0 اذن لا يمكن تطبيق التجميعية على A و B
نأخذ النقطتين (A;2) ; (D;2) لان
2+2=4≠0 اذن يقبلان مرجحا نرمز له ب H ومنه فان G مرجح النقط (H;4) ; (B;-2) ; (C;1)
يمكن ان نطبق التجميعية ايضا على النقطتين B; C لان
-2+1=-1≠0 اذن يقبلان مرجحا نرمز له ب T
ومنه فان G مرجح للنقطتين (H;4) ; (T;-1)
ملاحظة يمكن رسم المرجح G برسم كل من H و T
لدينا H مرجح ل (A;2) ; (D;2) يعني
∀M: 2MA→+2MD→=4MH→
⇔
∀M: MA→+MD→=2MH→
وهذا يعني ان H منتصف القطعة [AD]
ولدينا T مرجح ل (B;-2) ; (C;1) يعني
∀M: -2MB→+MC→=-MT→
⇔
BT→=-BC→
ونعلم ان
∀M: 2MA→+2MD→-2MB→+MC→=3MG→
⇔
4MH→-MT→=3MG→
⇔
-HT→=3HG→
وبالتالي
| HG→ = - | 1 | HT→ |
| 3 |
تمرين 6 tp
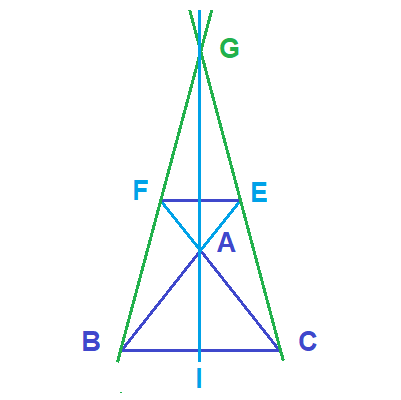
لتكن G مرجح النقط المتزنة (A;-3) ; (B;1) ; (C;1) ولتكن E نقطة بحيث AB→=-2AE→ ونعتبر F مسقط E على (AC) في اتجاه (BC)
1) انشئ الشكل
2) بين ان
| AF→ = | 1 | AC→ |
| 2 |
3) بين ان G تنتمي الى المستقيم المار من A ومن I منتصف القطعة [BC]
4) بين ان IG→=3IA→
5) بين ان المستقيمات (CE); (BF) ; (AI) متلاقية في المرجح G
تصحيح
1)
2) نعلم ان الاسقاط يحافظ على معامل استقامبة متجهتين
لدينا AB→=-2AE→
و A; C; F المساقط على التوالي للنقط A; B; E على المستقيم (AC) في اتجاه (BC) اذن
| AC→=-2AF→⇔ AF→ = - | 1 | AC→ |
| 2 |
3) لدينا G مرجح النقط المتزنة (A;-3) ; (B;1) ; (C;1)
بما ان
1+1=2≠0 فان النقطتين (B;1) ; (C;1) تقبلان مركز ثقل اي منتصف القطعة [BC] ونرمز له ب I ;ومنه فان G مرجح النقطتين المتزنتين (A;-3) ; (I;2) وبالتالي G∈(AI)
4) نبين ان IG→=3IA→
لدينا G مرجح (A;-3) ; (I;2)
اذن
-3GA→+2GI→=O→ ⇔-3GI→-3IA→+2GI→=O
⇔ -GI→=+3IA→
⇔ IG→=3IA→
5) نعلم ان AB→=-2AE→
⇔ GB→-GA→=-2(GE→-GA→)
⇔ GB→-3GA→=-2GE→
⇔ -GC→=-2GE→
⇔ GC→=2GE→
اذن G∈(CE)
وبنفس الطريقة يمكن ان نبين ان G∈(BF)
وبالتالي G∈(AI)∩(CE)∩(BF).
تمرين 7 tp
نعتبر في المستوى المنسوب الى معلم متعامد ممنظم
(O;i→;j→)
النقط A(5;2); B(3;1); C(1;5) و D
1) هل النقط (B;-4); (C;7); (D;-3)
تقبل مرجحا G ?
2) بين ان (A;-2) ; (B;4); (C;3), تقبل مرجحا G
3) حدد G(xG;yG).
تصحيح
1) لدينا
-4+7-3=0 اذن (B;-4); (C;7); (D;-3) لا تقبل مرجحا
2) لدينا
-2+4+3=5≠0 اذن (A;-2) ; (B;4); (C;3) تقبل مرجحا G
3) نحدد احداتيتي G.
| { | xG = | -2.5+4.3+3.1 | ; G(1;3) |
| -2+4+3 | |||
| yG = | -2.2+4.1+3.5 | ||
| -2+4+3 |
تمرين 8 tp
نعتبر في المستوى المنسوب الى معلم متعامد ممنظم
(O;i→;j→)
نقطتين A(-1;5) و B(3;4)
1) بين ان (A;2) و (B;8) تقبلان مرجحا G
2) حدد G(xG;yG).
تصحيح
1) لدينا
2+8=10≠0 اذن A و B تقبلان مرجحا G.
2) نحدد احداتيتا G.
| { | xG = | 2.(-1)+8.3 |
| 2+8 | ||
| yG = | 2.5+8.4 | |
| 2+8 |
اذن G(2,2 ; 5,2).