الاشتقاق (1)
1- الاشتقاق في نقطة والتاويل الهندسي للعددالمشتق
1.1 الاشتقاق في نقطة
1.1.1 تعريف
لتكن f دالة عددية معرفة على مجال I ; a∈I
نقول ان الدالة f قابلة للاشتقاق في نقطة a
يعني يوجد عدد حقيقي L بحيث
|
lim x→a |
f(x)-f(a) | =L | |
| x-a |
العدد L يسمة العدد المشتق للدالة f في النقطة a ,
ونرمز له ب f'(a)
ونكتب
|
lim x→a |
f(x)-f(a) | =f'(a) | |
| x-a |
1.2 التاويل الهندسي
1.2.1 تقديم
لتكن f دالة قابلة للاشتقاق في a
اذن:
| lim x→a |
f(x)-f(a) | =f'(a) | |
| x-a |
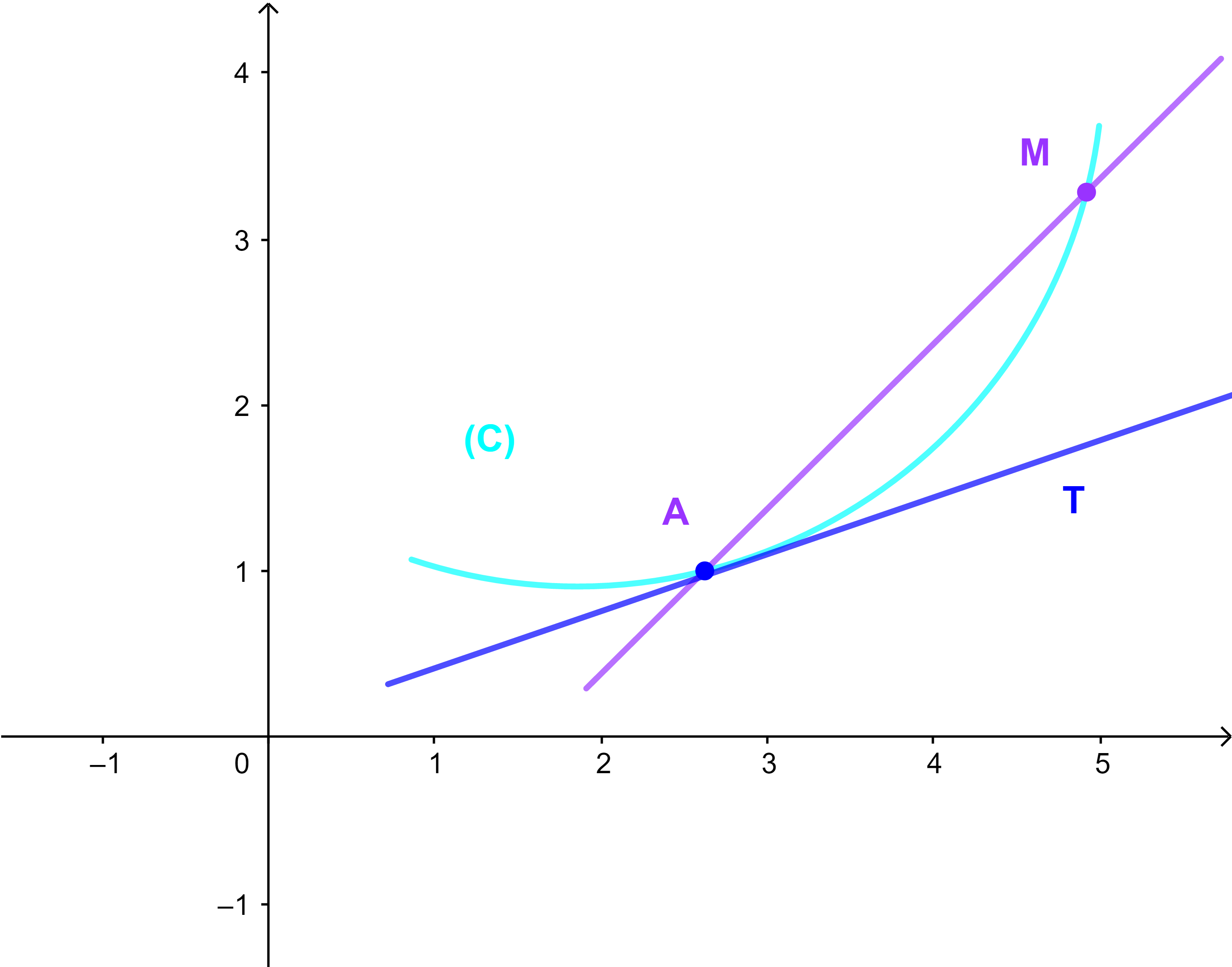
يكن (C) المنحنى الممثل للدالة f
و A(a;f(a))∈(C).
اذا كانت M(x;y)∈Cf, فان العدد
| f(x)-f(a) | |
| x-a |
هو المعامل الموجه للمستقيم (AM), واذا كانت النقطة M تنتقل على المنحنى الى ان تنطبق مع النقطة A, فان المستقيم (AM) ياخذ وضعية وحيدة هي وضعية المستقيم (T) الذي يمس المنحنى في نقطة واحدة A=M.
ميله العدد
| lim x→a | f(x)-f(a) | =f'(a) | |
| x-a |
اذن المستقيم (T) معادلته هي
y=f'(a)(x-a)+f(a)
ويسمى مماسا
للمنحنى (C) في النقطة A .
مثال 1
f(x)=x²
f قابلة للاشتقاق في 1
ثم حدد معادلة المماس عند النقطة A(-2;f(-2))
مثال 2
f(x)=x³
بين ان f قابلة للاشتقاق في 1
ثم حدد معادلة المماس عند النقطة A(1;f(1)).
تصحيح
|
lim x→1 |
f(x)-f(1) | = | lim x→1 | x³-1³ |
| x-1 | x-1 | |||
|
lim x→1 |
f(x)-f(1) | = | lim x→1 |
(x-1)(x²+x+1) |
| x-1 | x-1 |
= limx→2 (x²+x+1) =4
وهذا يعني ان الدالة قابلة للاشتقاق في 1 والعدد المشتق هو f'(1)=4
وبالتالي الدالة f تقبل مماسا عند A(1;1) معادلته هي
T: y=f'(1)(x-1)+f(1)
T: y=4x-3.
تقريب تآلفي
لتكن f دالة قابلة للاشتقاق في a
الدالة x→f'(a)(x-a)+f(a) هي تقريب تآلفي للدالة f في النقطة a
(اي f(a+h)≃hf'(a)+f(a); h→0)
تمرين
لتكن f دالة عددية معرفة ب f(x)=√(x)
1)حدد التقريب التآلفي f(1+h)
بجوار
0 ?
2) تطبيق: حدد قيمة مقربة للعدد √(1,005)
تصحيح
لدينا : f(a+h)≃hf'(a)+f(a); h→0
و f(1)=1 اذن يجب حساب العدد المشتق f'(1)
| lim x→1 |
f(x)-f(1) | ||
| x-1 | |||
| = | lim x→1 | 1 | |
| √(x)+1 |
اذن f'(1)=0,5
وبالتالي f(1+h)≃(0,5)h+1
لاحظ ان √(1,005)=√(1+0,005)
0,005 يقترب من
0 والدالة x→√(x)
قابلة للاشتقاق في 1 اذن
f(1+0,005)≃0,005f'(1)+f(1)
اي √(1,005)≃0,005×(0,5)+1
ومنه فان √1,005 ≃1,0025 .
2- الاشتقاق على مجال
2.1 تعاريف
نقول ان الدالة
f
قابلة للاشتقاق على المجال I, (I⊂Df)
يعني ان الدالة f قابلة للاشتقاق في كل نقطة من المجال I.
ونعني بالدالة المشتقة للدالة f على المجال I, والتي نرمز لها ب f',
الدالة التي تربط كل عنصر من x I بالعدد المشتق f'(x).
2.2 مشتقة الدوال :x→a, x→ax و x→xn
2.2.1 خاصيات
لتكن f دالة عددية ذات المتغير x
a∈IR; n∈IN*
f' الدالة المشتقة للدالة f.
اذا كان f(x)=a فان f'(x)=0
اذا كان f(x)=ax فان f'(x)=a
اذا كان f(x)=xn فان f'(x)=nxn-1
نبين ان (ax)'=a
نبين ان f قابلة للاشتقاق في عدد مثلا b.
| lim x→b |
f(x)-f(b) | = | lim x→b |
ax-ab |
| x-b | x-b | |||
| = | lim x→b |
a(x-b) | = a | |
| x-b |
اذن f قابلة للاشتقاق في b وبالتالي f قابلة للاشتقاق في كل عدد حقيقي x ومنه فان الدالة f قابلة للاشتقاق على IR ودالتها المشتقة هي الدالة للثابتة f' المعرفة ب f'(x)=a
نبين ان (x²)=2x.
| lim x→b |
f(x)-f(b) | = | lim x→b |
x²-b² |
| x-b | x-b | |||
| =lim x→b |
(x+b)(x-b) | = | lim x→b |
x+b=2b |
| x-b |
اذن f قابلة للاشتقاق في b وبالتالي f قابلة للاشتقاق في كل عدد حقيقي x ومنه فان الدالة f قابلة للاشتقاق على IR ودالتها المشتقة هي الدالة
f' المعرفة ب f'(x)=2x
ونعمم (xn)'=nxn-1 حيث n∈IN*
مثال 1
1) f(x)=5⇒ ∀x∈IR, f'(x)=0
2) f(x)=-17⇒ ∀x∈IR, f'(x)=0
مثال 2
f(x)=x²
f قابلة للاشتقاق على IR
∀x∈IR, f'(x)=2x
مثال 3
f(x)=x³
f قابلة للاشتقاق على IR
∀x∈IR, f'(x)=3x²
مثال 4
f(x)=x4
f قابلة للاشتقاق على IR
∀x∈IR, f'(x)=4x³
مثال 5
f(x)=x5
f قابلة للاشتقاق على IR
∀x∈IR, f'(x)=5x4.