Dérivation (1)
1- Dérivation et fonction dérivée
1.1 Dérivabilité en un point
1.1.1 Définition
Soient f une fonction définie sur un intérvalle I et a∈I.
f est dérivable au point a signifie qu'il existe
un nombre réel L tel que
lim x→a |
f(x)-f(a) | = L |
| x-a |
L est le Nombre dérivé de f en a, noté f'(a).
| On écrit | lim x→a |
f(x)-f(a) | = f'(a) |
| x-a |
Remarque si on pose h=x-a on obtient
lim x→a |
f(x)-f(a) | = | lim h→0 | f(a+h)-f(a) |
| x-a | h |
1.1.2 Interprétation géométrique
Le plan est rapporté à un repère orthonormé (O;i→;j→). On considère une fonction f dérivable au point a et (C) sa courbe représentative
| donc | lim x→a |
f(x)-f(a) | = f'(a) | |
| x-a |
Soient A(a ; f(a)) et M(x;y) deux points de la courbe (C).
| Le nombre | f(x)-f(a) | |
| x-a |
est le coefficient directeur de la droite (AM).
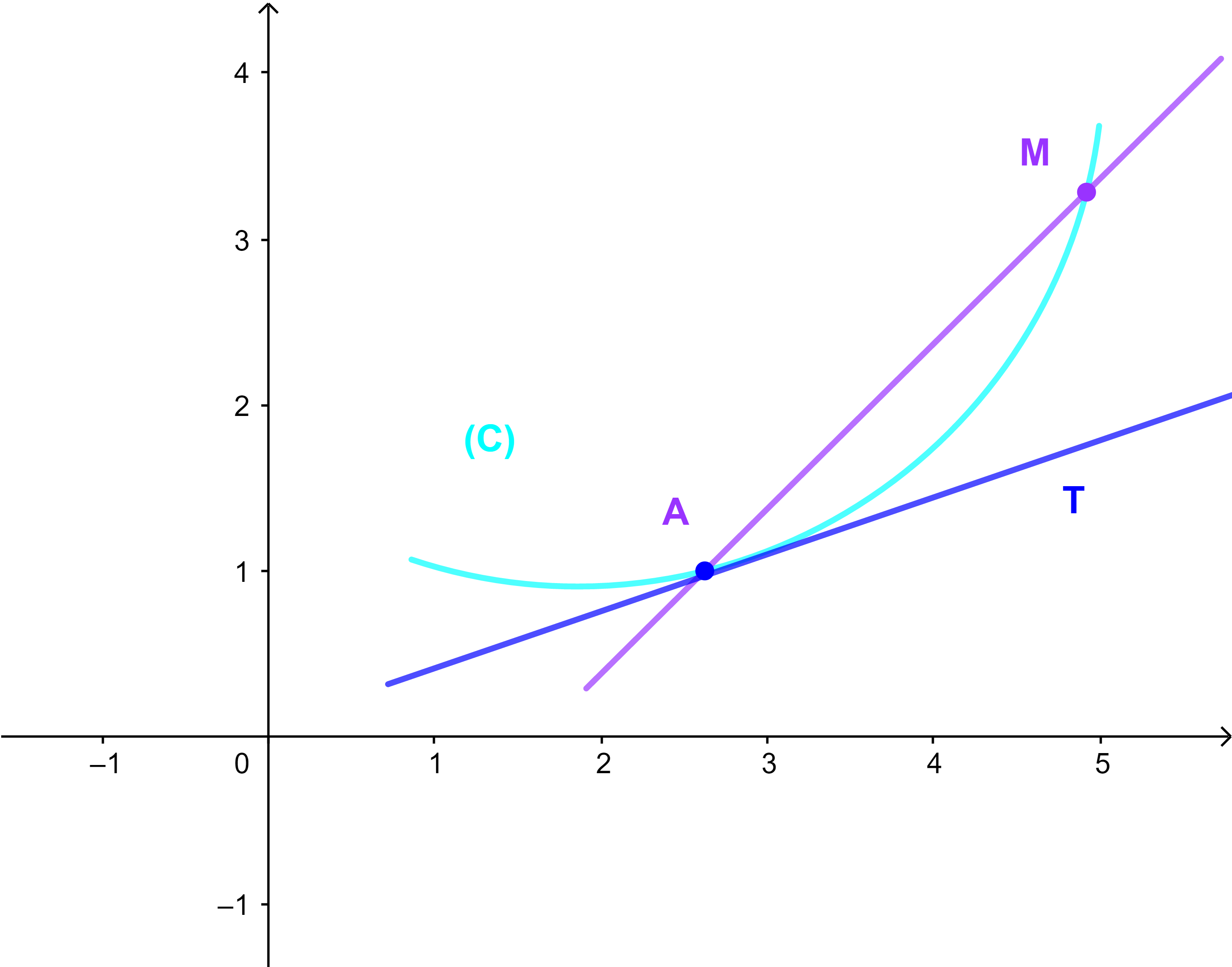
De plus si M se déplace sur la courbe jusqu'elle se confonde avec A alors la droite (AM) prend une disposition unique, la droite (Δ) qui coupe la courbe en un seul point A=M et son coefficient directeur est la limite suivante
lim x→a |
f(x)-f(a) | = f'(a) | |
| x-a |
Et donc la droite (Δ) d'équation
y=f'(a)(x-a)+f(a) est appelée tangente
à la courbe (C) au point A.
1.2.2 Propriétés et Définitions
Soit f une fonction dérivable au point a.
1) Elle existe une fonction g telle que
f(x)=f'(a)(x-a)+f(a)+(x-a)g(x).
2) y=f'(a)(x-a)+f(a) est l'équation de la tangente à la courbe (C) au point A(a;f(a)).
3) La fonction x→f'(a)(x-a)+f(a) est
l'Approximation affine
de la fonction f au point a.
(ou f(a+h)≃hf'(a)+f(a) quand h→0).
Exercice 1 tp
Soit f une fonction définie par f(x)=x³.
1) Montrer que f est dérivable au point 1.
2) Déterminer l'équation de la tangente au point A(1;f(1)).
Correction
lim x→1 |
f(x)-f(1) | = | lim x→1 |
x³-1³ |
| x-1 | x-1 | |||
| lim x→1 |
f(x)-f(1) | = | lim x→1 |
(x-1)(x²+x+1) |
| x-1 | x-1 |
| = | lim 1 | (x²+x+1) = 3 |
donc f est dérivable au point 1 et f'(1)=3 est le nombre dérivé au point 1
ainsi la courbe (C) admet une tangente au point A(1;1) d'équation
T: y=f'(1)(x-1)+f(1)
ou encore T: y=3x-2.