2- المستقيم المتجهي والمستوى المتجهي

2.1 المستقيم المتجهي

2.1.1 استقامية متجهتين

u^→ و v^→ متجهتان مستقيميتان اذا وفقط اذا وجد عدد حقيقي k بحيث v^→=ku^→.

2.1.2 استقامية النقط

A; B و C ثلاث نقط مستقيمية اذا وفقط اذا AB^→ و AC^→ مستقيميتين.
بعبارة أخرى A و B و C ثلاث نقط مستقيمسة اذا وفقط اذا وجد عدد حقيقي k بحيث AC^→=kAB^→.

2.1.3 تعريف

لتكن A و B نقطتنين مختلفتين.
كل متجهة غير منعدمة u^→ ومستقيمية مع AB^→ هي متجهة موجهة للمستقيم (AB).

2.1.4 خاصية

لتكن A نقطة من الفضاء و u^→ متجهة غي منعدمة مجموعة نقط الفضاء M بحيث AM^→=ku^→ مع k∈IR هي المستقيم D(A;u^→) المار من A و u^→ متجهة موجهة له
D(A;u^→)={M∈E/ AM^→=ku^→; k∈IR}.

2.2 المستوى المتجهي

2.2.1 تعريف

ليكن ℙ مستوى من الفضاء و.
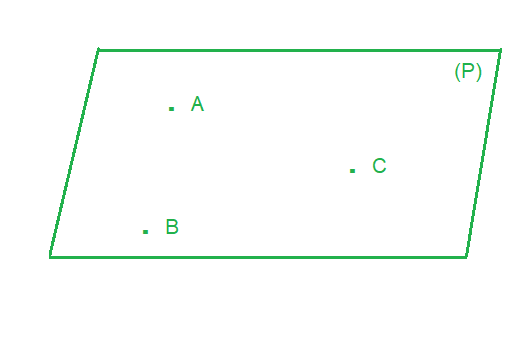
اذا كانت A و B و C نقطا غير مستقيمية في المستوى ℙ فان
ℙ هو المستوى المار من النقطة A وموجه بالمتجهتين AB^→ و AC^→.

2.2.2 نتيجة

كل متجهتين غير مستقيميتسن u^→ و v^→ ونقطة A من الفضاء تحدد مستوى مار من A وموجه بالمتجهتين u^→ و v^→.

2.2.3 خاصية

لتكن u^→ و v^→ متجهتين غير مستقيميتين و A نقطة من الفضاء
مجموعة نقط الفضاء M بحيث AM^→=ku^→+tv^→ مع k;t∈IR هي مستوى ℙ مار من A وموجه بالمتجهتين u^→ و v^→ ونكتب ℙ=ℙ(A;u^→;v^→)
ℙ={M∈(E)/ AM^→= ku^→+tv^→, k;t∈IR}.

2.3 الاستواء

2.3.1 تعريف 1

نقول ان اربع نقط او اكثر مستوائية اذا وجدت في نفس المستوى.

2.3.2 تعريف 2

نقول ان u^→; v^→ و w^→ مستوائية اذا وجدت اربع نقط مستوائية A; B; C و D في الفضاء بحيث
u^→=AB^→; v^→=AC^→ ; w^→ =AD^→.

بتعبير آخر u^→; v^→ و w^→ مستوائية اذا
∃A;B;C;D∈(𝔼):
u^→=AB^→ و v^→=AC^→ و w^→=AD^→ و D∈(ABC).