Exercice 1 tp

Soit TABC un tétraèdre dont toutes les faces sont des triangles équilatéraux.
Montrer que TC^→⊥AB^→ ; TB^→⊥AC^→ et TA^→⊥BC^→.

Correction

1) On montre que TC^→ ⊥AB^→.
(a) On considère le triangle équilatéral TAB et I le milieu du segment [AB]
on a (AB)⊥(TI).

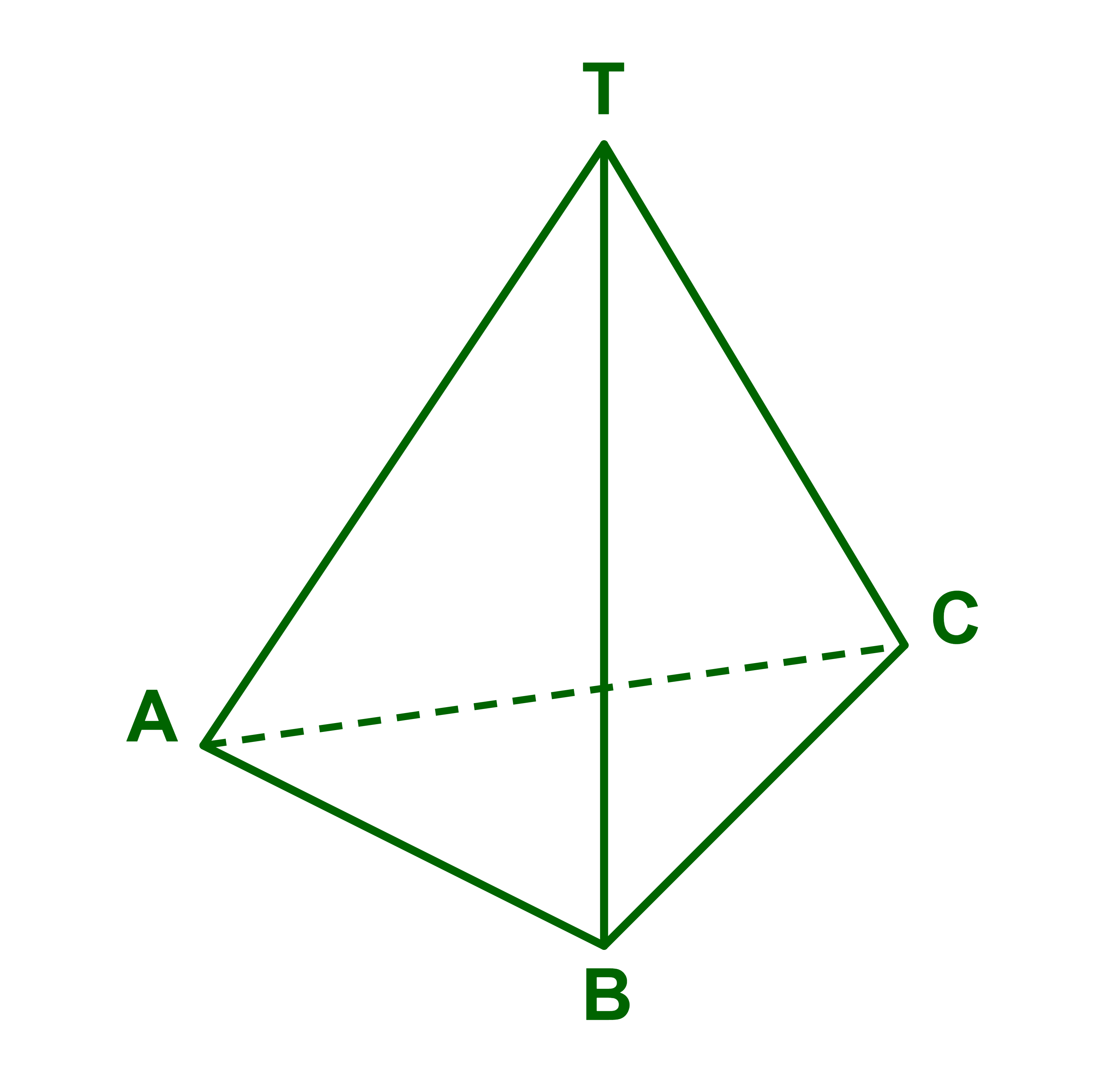
(b) On considère le triangle équilatéral ABC.

On a (AB)⊥(CI) donc

{	(AB)⊥(TI)	⇒ (AB)⊥(TCI)
	(AB)⊥(CI)

et on a

{	(TC)⊂(TCI)	⇒ (BD)⊥(TC)
	(AB)⊥(TCI)

donc TC^→ ⊥AB^→.

2) On montre que TB^→⊥AC^→.
(a) On considère le triangle équilatéral TAC et J le milieu du segment [AC]
on a (AC)⊥(TJ).
(b) On considère le triangle équilatéral ABC
on a (AC)⊥(BJ) donc

{	(AC)⊥(TJ)	⇒ (AC)⊥(TBJ)
	(AC)⊥(BJ)

Et on a

{	(TB)⊂(TBJ)	⇒ (AC)⊥(TB)
	(AC)⊥(TBJ)

ainsi TB^→⊥CD^→.
de la même manière on montre
TD^→⊥BC^→.

Exercice 2 tp

Soit TBCD un tétraèdre. On considère deux points I et J tels que

DI→ =	1	TB→		BJ→ =	1	BT→	+ BC→
	2				2

1) Tracer la figure.
2) Montrer que les points I; D; J et C sont coplanaires.
3) Montrer que le quadilatère IDJC est un parallélogramme.

Exercice 3 tp

Soit PABCD un pyramide, dont la base ABCD est un carré de centre O et toutes les autres faces sont des triangles équilatéraux.
On considère un point M du plan (ABC) tel que

OM→ =	1	AB→
	2

1) Déterminer le lieu géométrique du point M.
2) Soit N le milieu du segment [PM].
On suppose que le point M change dans le plan (ABC)
déterminer alors le lieu du point N avec ses éléments caractéristiques.