Vecteurs de l'espace (2)
Exercice 1 tp
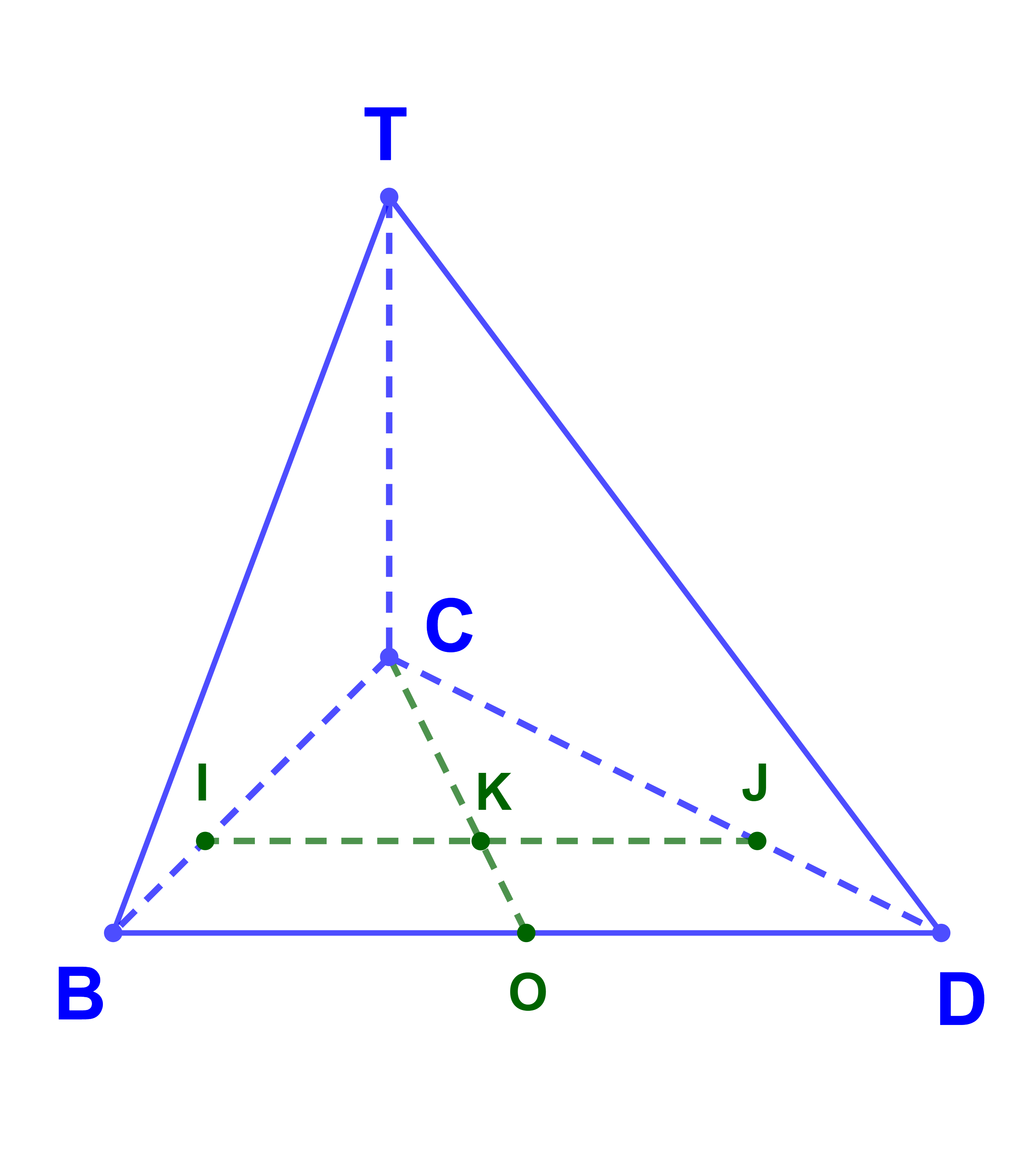
Soient TBCD un tétraèdre et O milieu du segment [BD].
On considère deux points I et J tels que
| BI→ = | 1 | BC→ | DJ→ = | 1 | DC→ | |
| 3 | 3 |
1) Montrer que les points I; J; T et D ne sont pas coplanaires.
2) Soit K un point tel que
| CK→ = | 2 | CO→ |
| 3 |
Montrer que K est le milieu du segment [IJ].
Correction
1) Supposons que I; J; T et D sont coplanaires
donc ils se trouvent sur le plan (IJD) car les point I; J et D ne sont pas alignés
et donc T∈(IJD)
ainsi les plans (TCD); (TBD) et (BCD) sont confondus et cela contraste avec le fait que (TBDC) est un tétraèdre
alors les points I; J; T et D ne sont pas coplanaires.
2) On montre que K est le milieu du segment [IJ]
on a
| CK→ = | 2 | CO→ |
| 3 |
ou encore
| CO→+OK→ = | 2 | CO→ |
| 3 |
| ⇒ OK→ = | 1 | OC→ |
| 3 |
On a
| { | OK→ = | 1 | OC→ |
| 3 | |||
| BI→ = | 1 | BC→ | |
| 3 |
On appliquz le théorème de Thalès sur le triangle CBO
on obtient
| KI→ = | 1 | OB→ |
| 3 |
On a aussi
| et { | OK→ = | 1 | OC→ |
| 3 | |||
| DJ→ = | 1 | DC→ | |
| 3 |
On applique sur le triangle COD le théorème de Thalès
on obtient
| KJ→ = | 1 | OD→ |
| 3 |
Puisque O est le milieu du segment [BD] alors OD→=-OB→ et donc
| KJ→ = | -1 | OB→= -KI→ |
| 3 |
ainsi
KI→=- KJ→
et cela signifie que K est le milieu du segment [IJ].