تحليلية الفضاء (1)
1- المعلم في الفضاء
1.1 احداثيات نقطة ومتجهة
1.1.1 تعريف
لتكن O نقطة من الفضاء و i→; j→ و
k→ ثلاث متجهات غي مستوائية
المربوع (O;i→;j→;k→)
معلم في الفضاء.
بالاضافة الى ذلك اذا كانت i→; j→ و k→ متعامدة مثنى مثنى و ||i→||=||j→||=||k→||=1 فان المعلم (O;i→;j→;k→) متعامد ممنظم.
1.1.2 احداثيات نقطة
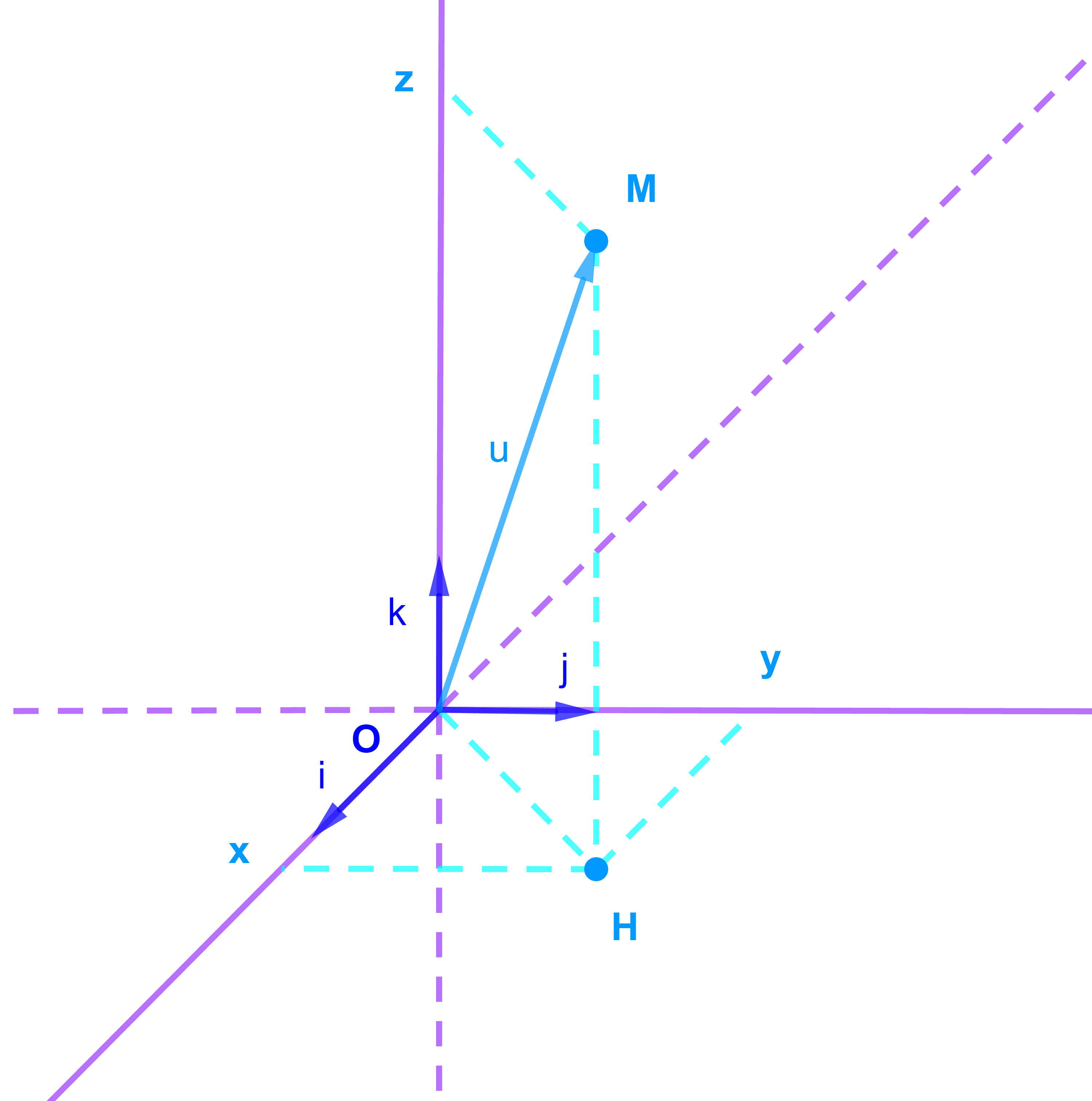
∀M∈(𝔼)∃(x;y;z)∈ℝ³:
OM→= xi→+yj→+zk→
ونكتب
| OM→ | x | أو OM→(x;y;z) |
| y | ||
| z |
x افصول ل M
y ارتوب ل M
z انسوب ل M
1.1.3 احداثيات متجهة في اساس
اساس في الفضاء
ثلاث متجهات غير مستوائية u→ و v→ و w→ تحدد اساسا في الفضاء
ونكتب (u→;v→;w→).
مثال
(O;i→;j→;k→)
معلم في الفضاء اذن (i→;j→;k→) اساس في الفضاء.
خاصية
ليكن B=(u→;v→;w→) اساسا
(∀e→∈V3)(∃(x;y;z)∈IR³):
e→=xu→+yv→+zw→
ونكتب e→B(x;y;z).
احداثيات u→+v→
ليكن (i→;j→;k→) اساسا في الفضاء.
نعتبر u→(x;y;z); v→(x';y';z') متجهتين.
لدينا u→+v→(x+x';y+y';z+z').
مثال
نعتبر u→(3;1;2); v→(-5;7;1) متجهتين.
لدينا u→+v→(-2;8;3).
احداثيات tu→
لتكن u→(x;y;z) متجهة و
t عددا حقيقيا.
لدينا tu→(tx:ty;tz).
مثال
نعتبر متجهة u→(5;-4;7)
لدينا -3u→(-15;12;-21).