Etude des fonctions numériques (10)
Exercice 1 tp
Soit f une fonction définie par
| f(x) = 2sinx + | 1 | cos2x |
| 4 |
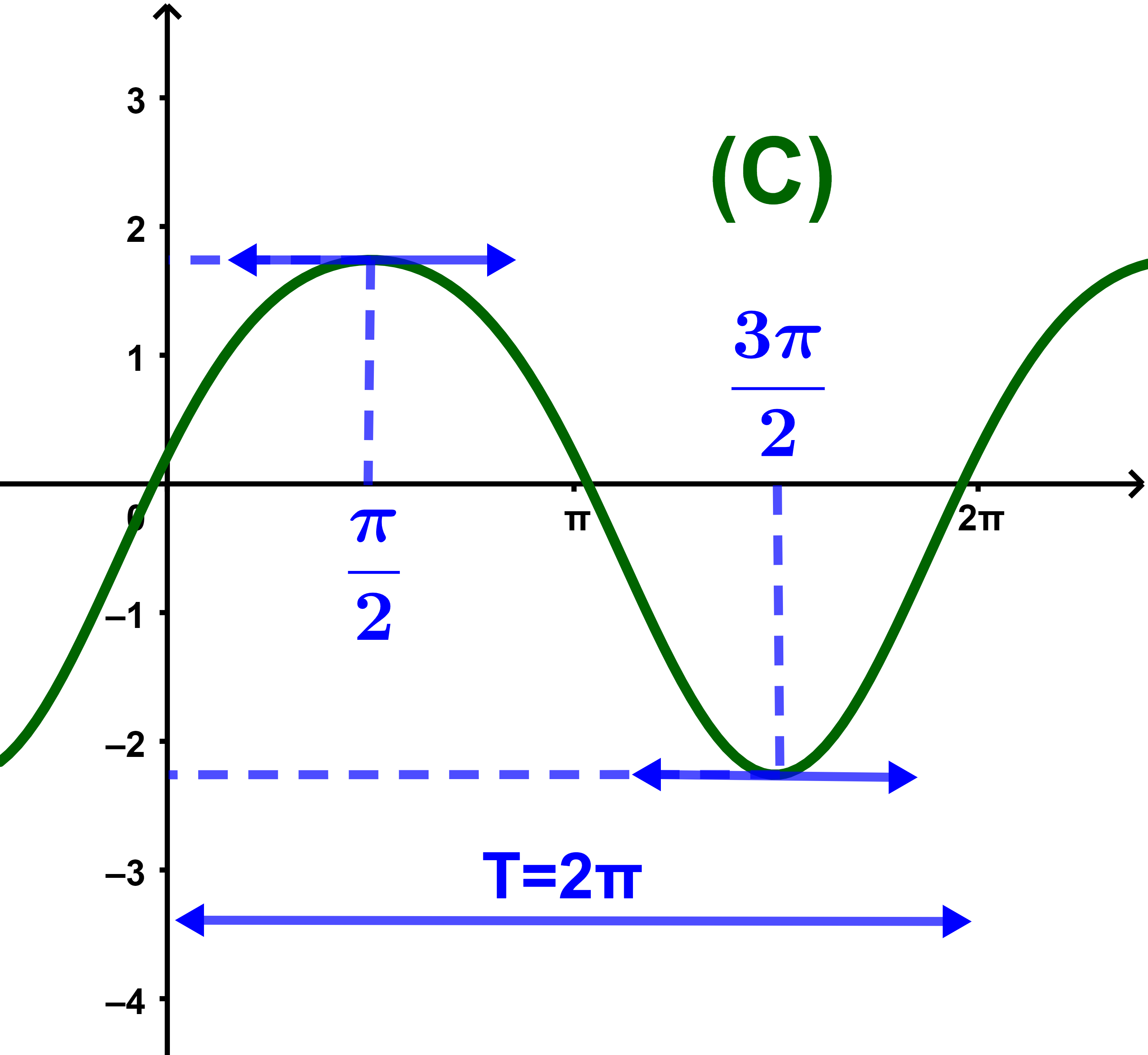
et (C) sa courbe dans un repère (O;i→;j→).
1) Montrer que f est périodique et déterminer I son domaine réduit d'étude.
2) Etudier la monotonie de f et tracer son tableau de variations sur [0;2π].
3) Tracer la courbe (C) sur [0;2π].
Correction
1) Les fonctions cos et sin sont définies sur IR et périodiques de période 2π.
La période de la fonction cos2x est π
mais la fonction f est une somme de deux fonctions périodiques
et donc la période la plus grande doit être prise.
On a D=IR donc (∀x∈IR): x+2π∈IR et x-2π∈IR.
| f(x+2π) = 2sin(x+2π) + | 1 | cos2(x+2π) |
| 4 |
| = 2sinx + | 1 | cos(2x+4π) |
| 4 | ||
| = 2sinx + | 1 | cos2x = f(x) |
| 4 |
f(x+2π)=f(x) signifie que f est périodique de période 2π
il suffit donc d'étudier f sur un intervalle d'amplitude 2π, soit I=[0;2π]
2) Les fonctions x→2x ; cos et sin sont dérivables sur IR donc f est dérivble sur IR et en particulier sur I.
Soit x∈I
f'(x)=2cos(x)-sin(x)cos(x) car sin2x=2sinxcosx
ainsi f'(x)=cos(x)(2-sinx)=0 ⇔ (cosx=0 ou sinx=2) ⇔ cosx=0 ⇔
x=π÷2[2π]
x∈I, ⇒ x=π÷2 ou x=3π÷2
2-sinx≥0 donc f' est de signe de cosx.
| x | 0 | π | 3π | 2π | |||
| 2 | 2 | ||||||
| f'(x) | + | 0 | - | 0 | + | ||
| f | 0,25 |
↗ |
1,75 | ↘ |
-2,25 |
↗ |
0,25 |
3) La courbe (C)