Etude des fonctions numériques (9)
Exercice 1 tp
Soit f une fonction définie par
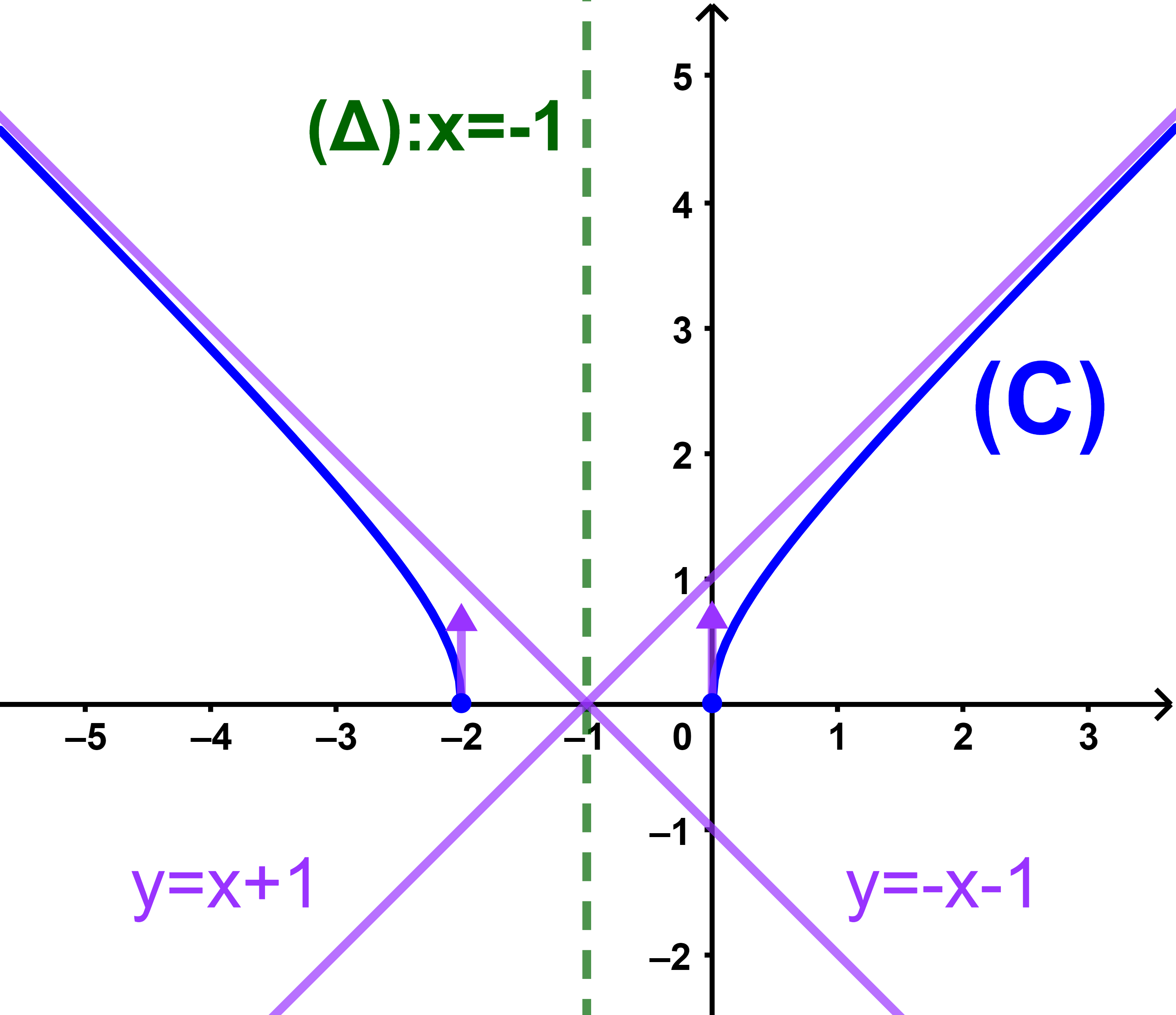
f(x)=√(x²+2x) et (C) sa courbe dans un repère orthonormé (O;i→;j→).
1) Montrer que la droite (Δ1): x=-1 est un axe de symétrie de (C) et déduire le domaine réduit de f.
2) Calculer la limite de f en +∞ et montrer que la droite (Δ2): y=x+1 est une asymptote oblique à (C) au voisinage de +∞.
3) Etudier la dérivabilité de f en 0.
4) (a) Montrer que (∀x∈D\{-2;0})
| f '(x) = | x+1 |
| √(x²+2x) |
et déduire les variations de f.
(b) Tracer le tableau de variations de f sur D.
5) Tracer la courbe (C).
Correction
1) Notons que (Δ): x=a est un axe de symétrie d'une courbe
signifie (∀x∈D): 2a-x∈D et f(2a-x)=f(x).
D={x∈IR / x²+2x≥0}
=]-∞;-2]∪[0;+∞[.
Soit x∈D donc x∈]-∞;-2] ou x∈[0;+∞[.
Si x∈]-∞;-2] alors x≤-2 ou encore -x≥2
ou encore -2-x≥0
donc 2.(-1)-x∈[0;+∞[ ainsi 2.(-1)-x∈D.
Si x∈[0;+∞[ alors x≥0 ou encore -x≤0 ou encore -2-x≤-2
Donc 2.(-1)-x∈]-∞;-2] ainsi 2.(-1)-x∈D
alors (∀x∈D): 2.(-1)-x∈D.
Soit x∈D: f(-2-x)=√((-2-x)²+2(-2-x))
=√(4+4x+x²-4-2x)
=√(x²+2x)
donc f(-2-x)=f(x) et cela signifie que (Δ1):x=-1 est un axe de symétrie de la courbe (C)
il suffit donc d'étudier f sur le domaine réduit
E=[0;+∞[.
| 2) | lim +∞ | x²+2x = | lim +∞ | x² = +∞ |
| ⇒ | lim +∞ | √(x²+2x) = +∞ |
| ainsi | lim +∞ | f(x) = +∞ |
Montrons que la droite (Δ2): y=x+1 est une asymptote oblique à (C) au voisinage de +∞.
La première condition est vérifiée
lim +∞ | f(x) = +∞ |
On calcule donc
lim +∞ |
f(x)-(x+1) = | lim +∞ | √(x²+2x)² - (x+1)² |
| √(x²+2x) + (x+1) |
lim +∞ | -1 | = | -1 | = 0 |
| √(x²+2x) + (x+1) | +∞ |
| Donc | lim +∞ | f(x)-(x+1) = 0 |
ainsi (Δ2):y=x+1 est une asymptote oblique à (C) au voisinage de +∞.
3) Dérivation à droite à 0
lim 0+ |
f(x)-f(0) | = | lim 0+ |
√(x²+2x) |
| x-0 | x |
| = | lim 0+ |
|x|√(1+2/x) | = | lim 0+ |
x√(1+2/x) |
| x | x |
| = | lim 0+ |
√(1+ | 2 | ) = +∞ |
| x |
| car | lim 0+ | 2 | = +∞ |
| x |
ainsi f n'est pas dérivable en 0
dans ce cas (C) admet une demi-tangente verticale au point O.
4) (a) Soit x∈D\{-2;0} donc x²+2x>0 et la fonction x→x²+2x est dérivable sur IR
elle est donc dérivable sur D\{-2;0}.
Soit x∈D\{-2;0}
| f '(x) = | (x²+2x)' | = | 2x+2 |
| 2√(x²+2x) | 2√(x²+2x) |
| ainsi f '(x) = | x+1 |
| √(x²+2x) |
Soit x∈D\{-2;0}.
f'(x) est de signe de x+1
| x | -∞ | -2 | -1 | 0 | +∞ | ||||
| x+1 | - | + | |||||||
ainsi f est strictement décroissante sur
]-∞;-2] et strictement croissante sur [0;+∞[.
Notons que la fonction f n'est pas définie sur ]-2;0[.
| x | -∞ | -2 | 0 | +∞ | |||||
| f '(x) | - | + | |||||||
| f | +∞ | ↘ |
0 |
0 |
↗ |
+∞ | |||
5) Puisque (Δ): x=-1 est un axe de symétrie de la courbe (C) alors on trace la courbe sur [0;+∞[ et on la complete en utilisant la symétrie axiale sur ]-∞;-2] d'axe (Δ).