Etude des fonctions numériques (10)
Exercice 1 tp
Soit f une fonction définie par
| f(x)= | √(1-x) - √(x+1) |
| x²-1 |
et (C) sa courbe dans un repère orthonormé (O;i→;j→).
1) Déterminer D, le domaine de définition de f
et étudier la parité de f.
2) Etudier le signe de g(x) sur D
g(x)=(1-3x)√(1-x) - (1+3x)√(1+x).
3) Calculer les limites suivantes
lim (-1)+ |
f(x) | lim 1- |
f(x) |
et déterminer les asymptotes de (C).
4) Montrer que ∀x∈D
| f '(x) = | g(x) |
| 2(x²-1)² |
et étudier le signe de f'(x) puis tracer le tableau de variations de f.
5) Tracer la courbe (C).
Correction
1) D={x∈IR/1-x≥0 ; x+1≥0 et x²-1≠0}
={x∈IR/ x > -1 et x< 1}
=]-1;1[0
D est centré en 0 donc
(∀x∈D) on a (-x)∈D.
| f(-x) = | √(1-(-x)) - √(-x+1) |
| (-x)²-1 |
| = | √(1+x) - √(1-x) |
| x²-1 | |
| = - | √(1-x) - √(1+x) |
| x²-1 |
Donc f(-x)=-f(x) et cela signifie que f est impaire.
2) Signe de g(x). Soit x∈D
g(x)=(1-3x)√(1-x) + (1+3x)√(1+x)
=(3x+1)√(1+x) - (3x-1)√(1-x)
On étudie le signe de g sur I car g est paire.
Soit x∈I=[0;1/3]∪[1/3;1[
Si x∈[1/3;1[ alors
3x+1>0 et 3x-1≥0
(3x+1≥3x-1) et (√(1+x)≥√(1-x))
⇒ (3x+1)√(1+x)>(3x-1)√(1-x)
⇒ g(x)>0.
Si x∈[0;1/3] alors
(3x+1>0) ; (1-3x≥0) et (√(1+x)≥√(1-x))
⇒ g(x)=(1-3x)√(1-x) + (1+3x)√(1+x)>0.
Conclusion
(∀x∈I): g(x)>0
et puisque g est paire alors (∀x∈D): g(x)>0.
3) Limite à gauche à 1
x<1 ⇒ x-1<0
| x | -1 | 1 | |
| x+1 | 0 | + | 2 |
| x-1 | -2 | - | 0 |
| x²-1 | 0 | - | 0 |
lim 1- |
f(x) | = | lim 1- |
√(1-x) - √(x+1) |
| x²-1 |
| = | - √(2) | = | + ∞ | ||
| 0- |
ainsi (C) admet une asymptote d'équation x=1 à gauche à 0.
Limite à droite à -1
lim (-1)+ |
f(x) | = | lim (-1)+ |
√(1-x) - √(x+1) |
| x²-1 |
| = | √(2) | = | - ∞ | ||
| 0- |
ainsi (C) admet une asymptote d'équation x=-1 à droite à 0.
4) La fonction dérivée f'
x→(x+1) et x→(1-x) sont strictement positives et dérivable sur D
donc x→√(x+1) et x→√(1-x) sont dérivable sur D
de plus la fonction x→(x²-1) ne s'annule pas et dérivable sur D alors f est dérivable sur D. Soit x∈D
| f(x) = | √(1-x) - √(x+1) |
| x²-1 |
| (√(1-x) - √(x+1))' = | -1 | - | 1 |
| 2√(1-x) | 2√(x+1) |
| = | -√(x+1) - √(1-x) |
| 2√(1-x²) | |
| = | (√(x+1) + √(1-x))√(1-x²) |
| 2(x²-1) |
donc f '(x) =
| (√(x+1)+√(1-x))√(1-x²)-4x(√(1-x)-√(x+1)) | |
| 2(x²-1)² |
| = | (1-3x)√(1-x)+(1+3x)√(1+x) |
| 2(x²-1)² |
donc ∀x∈D
| f '(x) = | g(x) |
| 2(x²-1)² |
f'(x) est de signe de g(x)
et puisque g est strictement positive sur D
alors (∀x∈D) on a f'(x)> 0
ainsi f est strictement croissante sur D.
| x | -∞ | +∞ | |
| f'(x) | + | ||
| f | -∞ |
↗ |
+∞ |
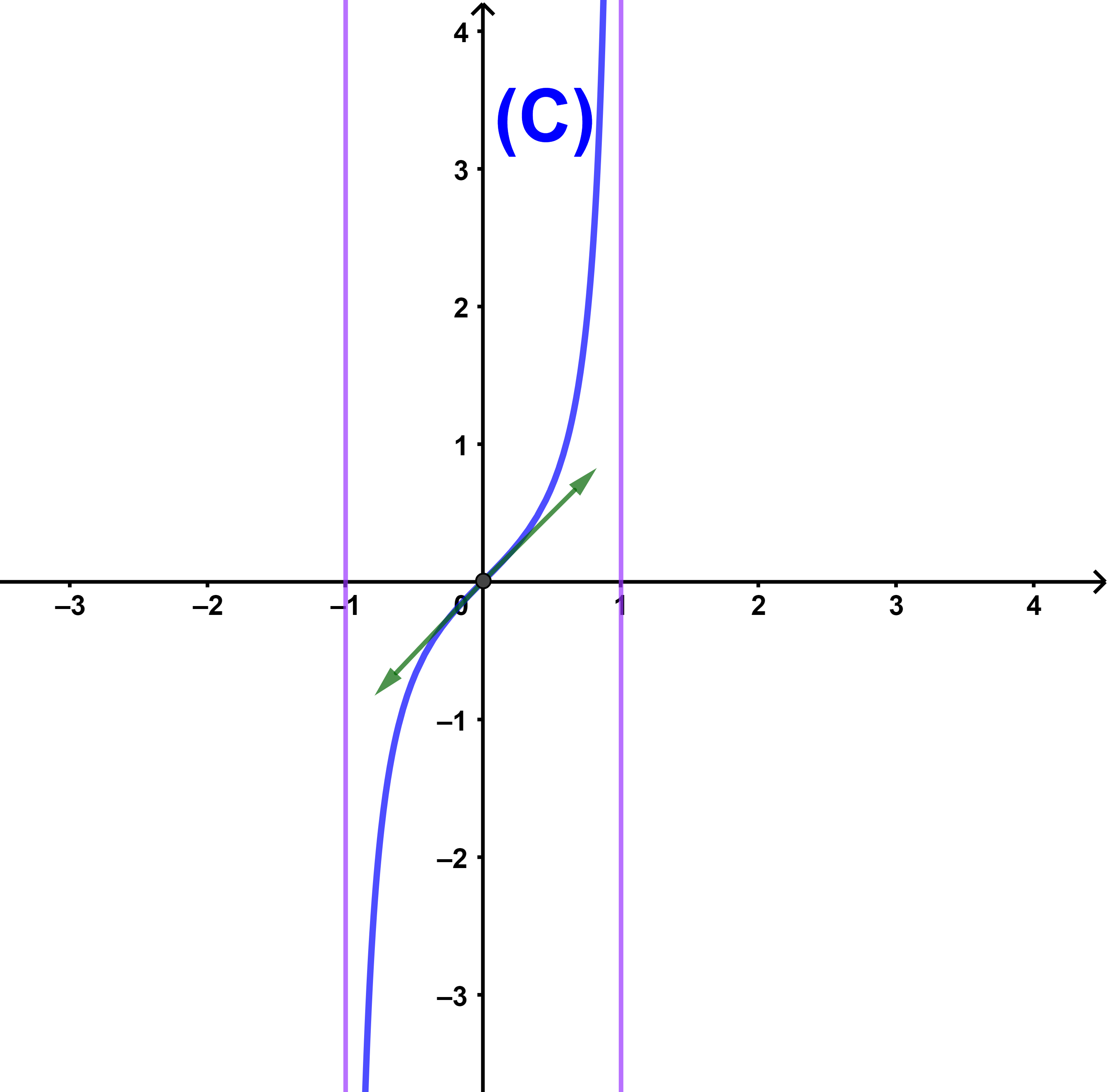
5) La courbe (C)