دراسة دوال عددية (8)
تمرين 14 tp
لتكن f دالة عددية معرفة كما يلي
| { | f(x)= | 2x | ; x≤0 |
| x²+1 | |||
| f(x)= | 2√(x) | ; x> 0 | |
| x²+1 |
(q2) احسب النهايات عند محدات مجموعة تعريف الدالة f
2) حدد مقاربات منحنى الدالة f
3) (q1) ادرس قابلية الاشتقاق الدالة f عند 0
(q2) ادرس رتابة الدالة f على المجالين ]-∞;0[ ; ]0;+∞[ وانشئ جدول التغيرات
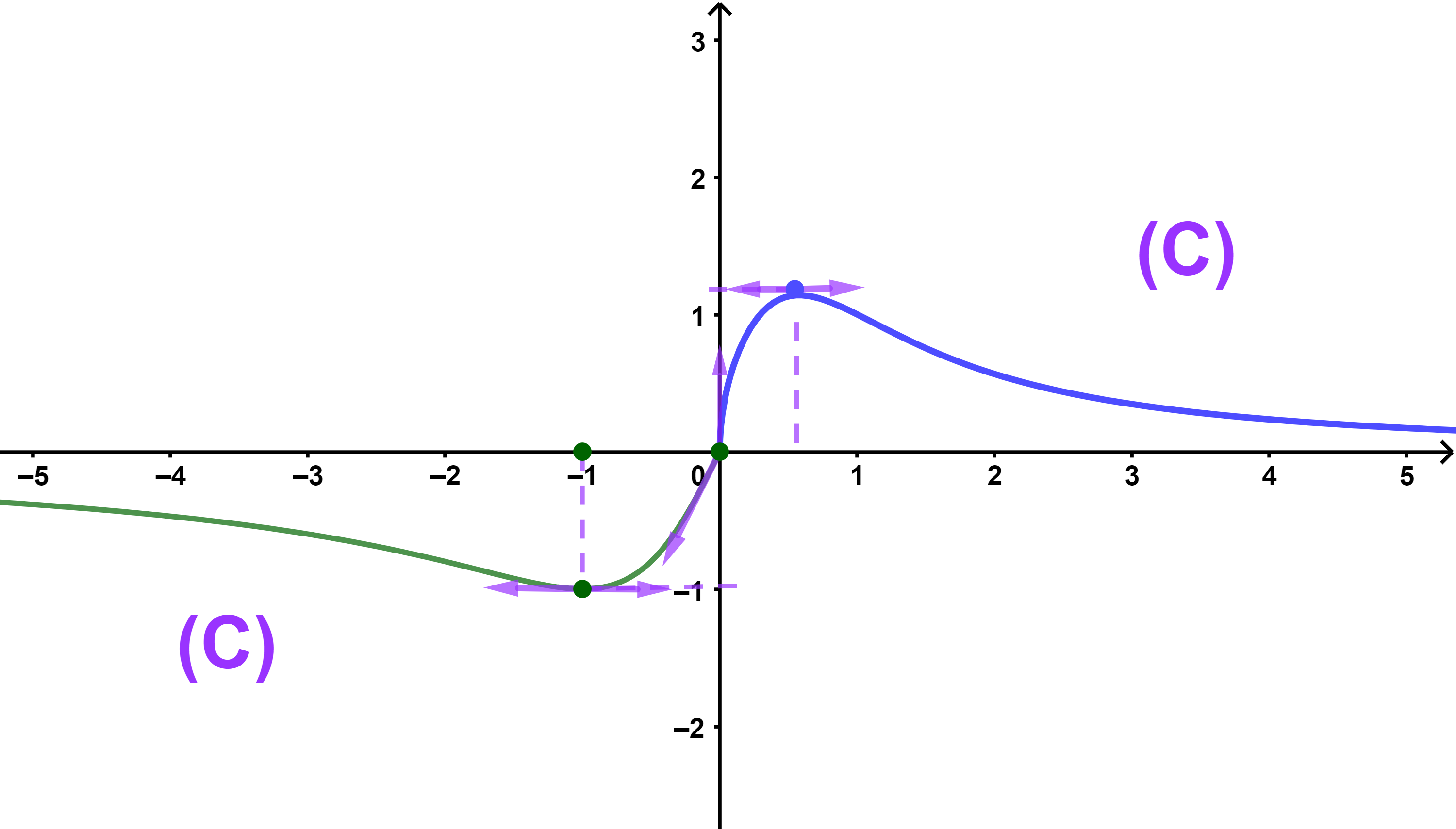
4) انشئ منحنى الدالة f في معلم متعامد ممنظم
5) حل مبيانيا وحسب قيم الوسيط m المعادلة f(x) = m
تصحيح
4) المنحنى
تمرين 15 tp
لتكن f دالة عددية معرفة كما يلي
| f(x)= | sinx |
| 1-cosx |
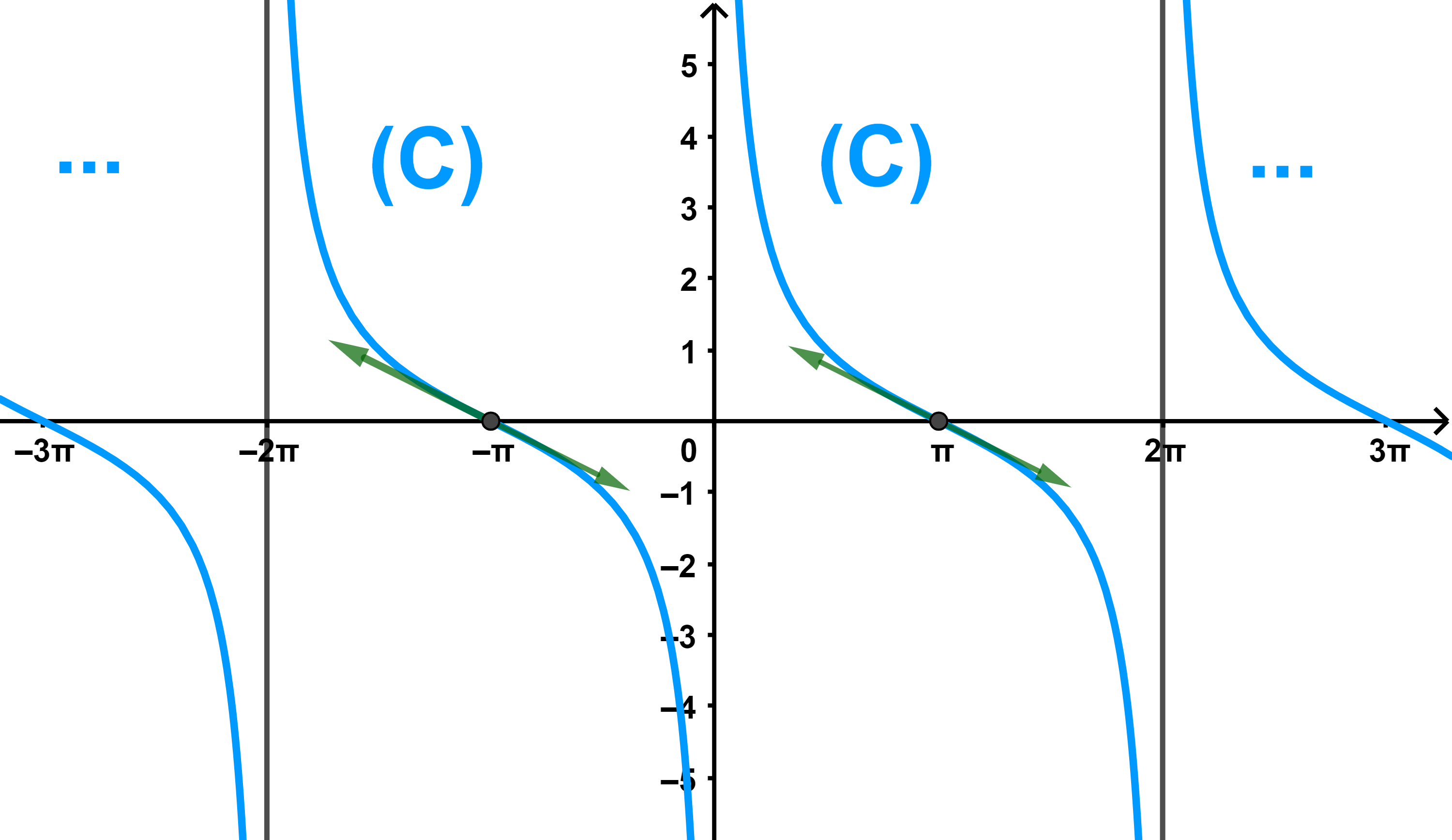
2) احسب نهاية الدالة f عند محدات المجال J ثم استنتج مقاربات منحنى الدالة f
3) ادرس رتابة الدالة f وانشئ جدول تغيراتها
4) انشئ منحنى الدالة f على المجال [-3π;3π]
تصحيح
1) D={x∈IR/ 1-cosx≠0}
={x∈IR/ x≠2kπ ; k∈ℤ}
لدينا ∀x∈D, x+2π;x-2π∈D
| f(x+2π)= | sin(x+2π) | = | sin(x) | = f(x) |
| 1-cos(x+2π) | 1-cos(x) |
∀x∈I, (-x)∈I
| f(-x)= | sin(-x) | = | - sin(x) | = -f(x) |
| 1-cos(-x) | 1-cos(x) |
2)
| lim 0+ |
f(x)= | lim 0+ |
sinx | |
| 1-cosx | ||||
| =lim 0+ |
1.sinx | . | x² | =+∞.1.2=+∞ |
| x.x | 1-cosx |
3) الدالتان cos و sin قابلتان للاشتقاق على IR وبالخصوص على J والدالة x→(1-cosx) لا تنعدم في J اذن f قابلة للاشتقاق على J
| f '(x)= | cosx(1-cosx)-sin²x |
| (1-cosx)² |
| = | -1+cosx |
| (1-cosx)² | |
| = | -1 |
| 1-cosx |
اذن ∀x∈J, f'(x)< 0 وبالتالي f تناقصية قطعا على J
| x | 0 | π | ||
| f '(x) | - | |||
| f | +∞ | ↘ | 0 |
|
4) نرسم المنحنى على J ثم نتممه باستعمال الازاحة ذات المتجهة 2πi→