دراسة دوال عددية (7)
تمرين 13 tp
نعتبر الدالة f المعرفة ب
| f(x)= | √(1-x) - √(x+1) |
| x²-1 |
2) ادرس اشارة g(x) على D حيث
g(x)=(1-3x)√(1-x) - (1+3x)√(1+x)
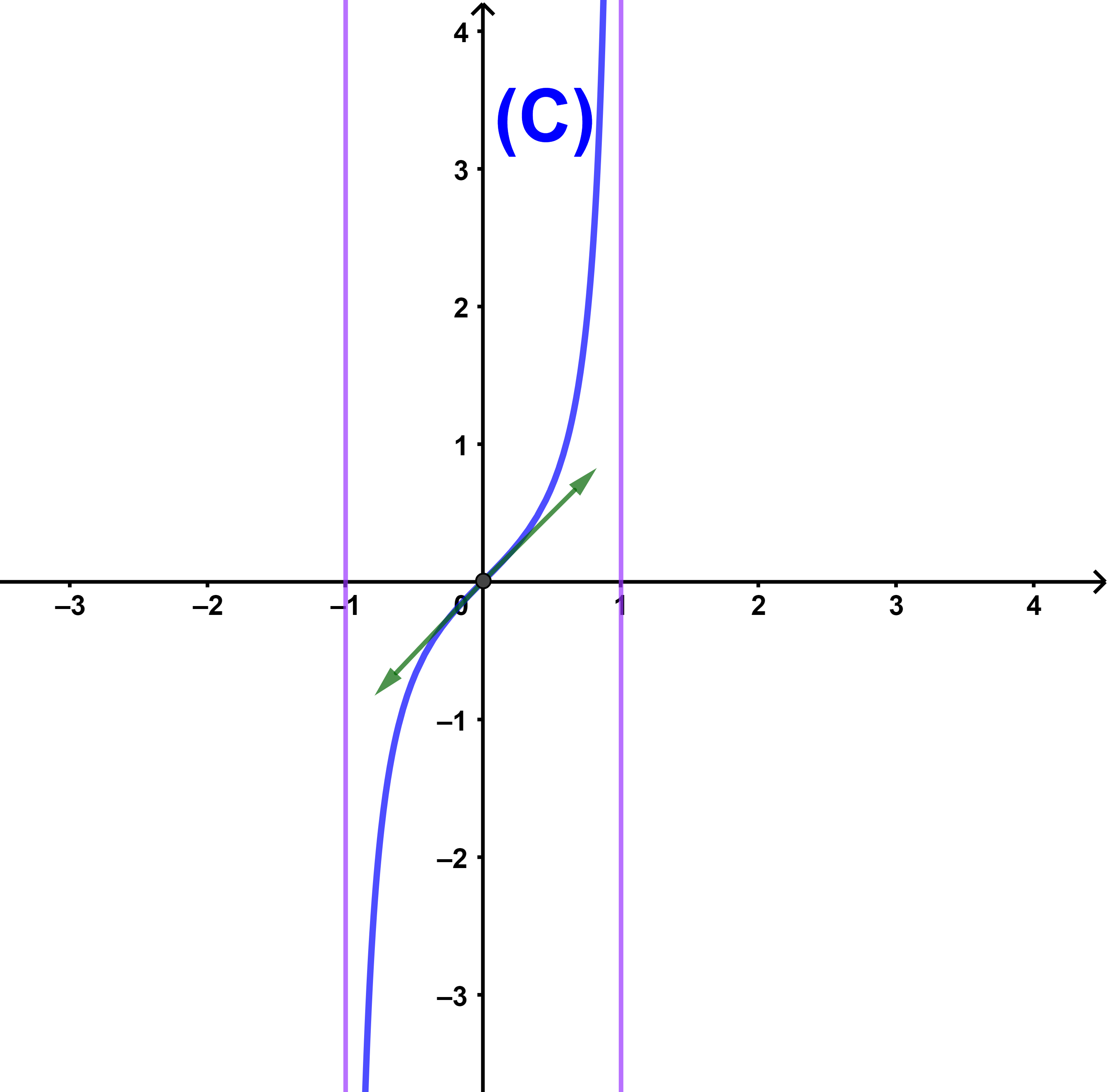
3) احسب نهايات الدالة f عند محدات مجموعة تعريفها ثم حدد المقاربين للمنحنى (C)
4) احسب f'(x) ثم ادرس اشارتها على مجموعة تعريفها وانشئ جدول تغيراتها
5) انشئ منحنى الدالة f في معلم متعامد ممنظم
تصحيح
1) D={x∈IR/1-x≥0 ∧ x+1≥0 ∧ x²-1≠0}
={x∈IR/ x> -1 ∧ x< 1}
=]-1;1[
المجال D مماثل بالنسبة للصفر اذن
∀x∈D, (-x)∈D
| f(-x)= | √(1-(-x)) - √(-x+1) |
| (-x)²-1 |
| = | √(1+x) - √(1-x) |
| x²-1 | |
| = - | √(1-x) - √(1+x) |
| x²-1 |
2)
g(x)=(1-3x)√(1-x) + (1+3x)√(1+x)
=(3x+1)√(1+x) - (3x-1)√(1-x)
نلاحظ ان الدالة g زوجية اذن يكفي دراسة اشارتها على المجال I
ليكن x∈I=[0;1/3]∪[1/3;1[ لدينا
اذا كان x∈[1/3; 1[ فان
3x+1>0 ∧
3x-1≥0
3x+1 ≥ 3x-1 ∧ √(1+x) ≥ √(1-x)
⇒ (3x+1)√(1+x) > (3x-1)√(1-x)
⇒ g(x) > 0
اذا كان x∈[0;1/3] فان
3x+1> 0 ∧ 1-3x≥0 ∧ √(1+x) ≥ √(1-x)
⇒ g(x)=(1-3x)√(1-x) + (1+3x)√(1+x)> 0
خلاصة
∀x∈I, g(x)> 0
وبما ان g دالة زوجية فان ∀x∈D, g(x)> 0
3) نحدد نهاية الدالة عند 1 على اليسار
x< 1 ⇒ x-1< 0
| x | -1 | 1 | |
| x+1 | 0 | + | 2 |
| x-1 | -2 | - | 0 |
| x²-1 | 0 | - | 0 |
| lim 1- |
f(x) | = | lim 1- |
√(1-x) - √(x+1) | |
| (x+1)(1-x) | |||||
| = | - √(2) | = | + ∞ | ||
| 0- |
نحدد نهاية الدالة f عند -1 على اليمين
| lim -1+ |
f(x) | = | lim -1+ |
√(1-x) - √(x+1) | |
| (x+1)(1-x) | |||||
| = | √(2) | = | - ∞ | ||
| 0- |
4) رتابة الدالة f
x→(x+1) و x→(1-x) دالتان موجبتان قطعا وقابلتان للاشتقاق على D
اذن x→√(x+1) و x→√(1-x) قابلتان للاشتقاق على D
ولدينا ايضا الدالة x→(x²-1) غير منعدمة وقابلة للاشتقاق على D وبالتالي f قابلة للاشتقاق على D
لدينا
| f(x)= | √(1-x) - √(x+1) |
| x²-1 |
| f '(x)= | (√(x+1) + √(1-x))√(1-x²) - 4x(√(1-x) - √(x+1)) |
| 2(x²-1)² | |
| f '(x)= | (1-3x)√(1-x) + (1+3x)√(1+x) |
| 2(x²-1)² | |
| f '(x)= | g(x) |
| 2(x²-1)² |
فان ∀x∈D, f'(x)> 0 اذن f تزايدية قطعا على D
5) المنحنى