1- عموميات حول الدوال

تمارين للتذكير

تمرين 1 tp

f دالة عددية معرفة كما يلي

f(x)=-2+	1
	x²+1

1) ادرس ؤتابة الدالة f
2) بين ان ∀x∈IR : f(x) > -2

تمرين 2 tp

f دالة عددية معرفة كما يلي f(x)=x²+2x+3
1. بين ان ∀x∈IR+: f(x)>2

تمرين 3

f دالة عددية معرفة كما يلي

f(x)=3-	1
	x

1) حدد D_f
2) بين ان ∀x∈R*+ : f(x)< 3

تمرين 4 tp

دالة عددية معرفة كما يلي f(x)=cosx
1) حدد D_f
2) بسط cos(x+2π) ثم cos(x-2π) واستنتج !

1.1 زوجية دالة ودورية دالة

1.1.1 تعريف الدالة الزوجية

نقول ان دالة زوجية اذا تحققت الشروط التالية
أ- مجموعة تعريفها مماثلة بالنسبة ل 0
x∈D, -x ∈D
ب- لكل عنصر من مجموعة التعريف ومقابله لهما نفس الصورة اي ∀x∈D, f(-x)=f(x)

مثال

الدالة
f: x→x²+5 زوجية

ملاحظة

اذا كانت دالة زوجية فان كل عنصر من مجموعة التعريف مقابله ايضا موجودا في مجموعة التعريف
لكل عنصر من مجموعة التعريف ومقابله لهما نفس الصورة بالدالة
اذا كانت دالة معرفة على مجموعة غير مماثلة بالنسبة ل 0 فان هذه الدالة ليست زوجية.

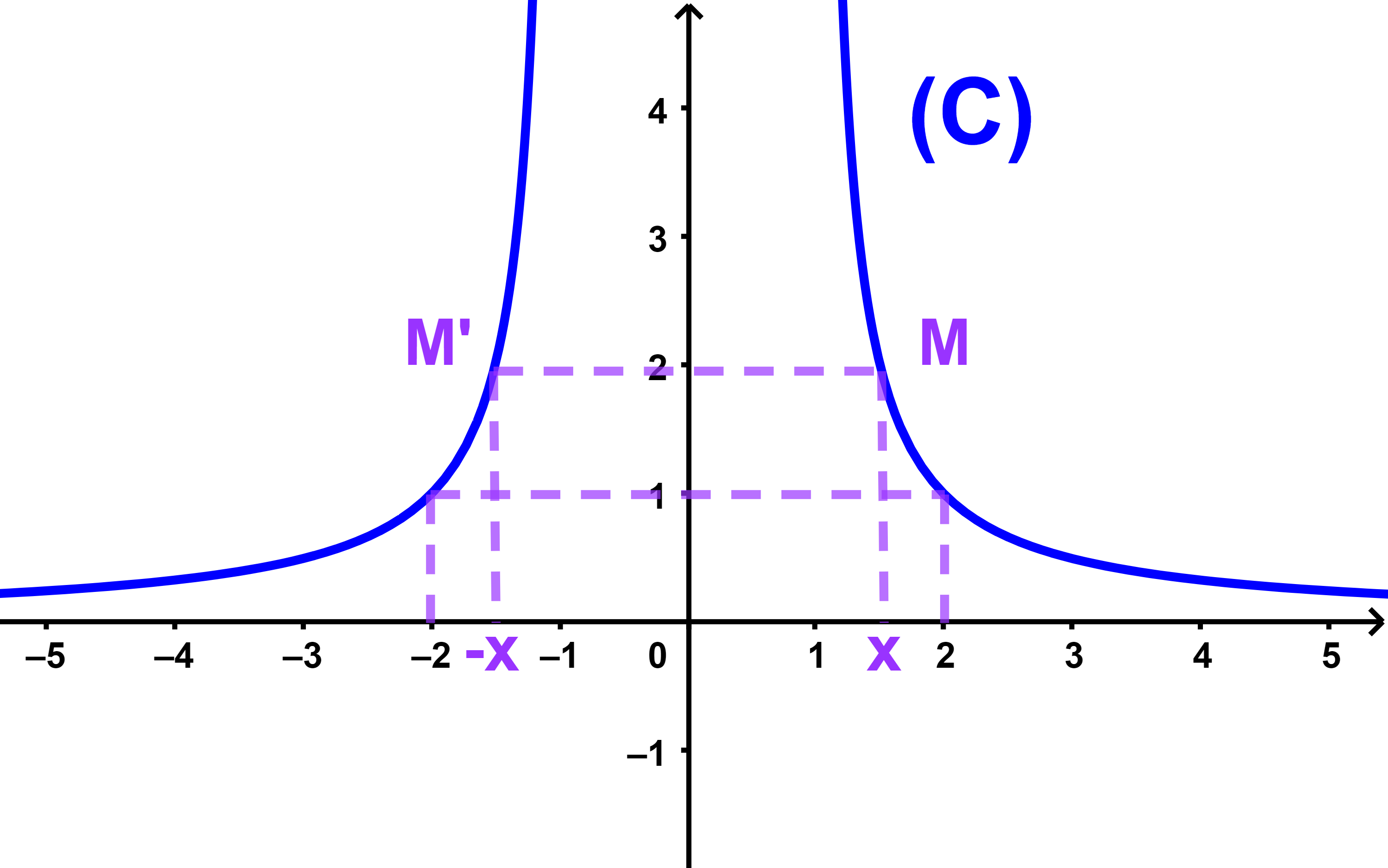
التمثيل المبياني

لتكن f دالة زوجية و C_f منحناها في معلم متعامد ممنظم (O;i^→;j^→).
x∈IR, f(-x)=f(x)⇒ M(x;f(x)) و M'(-x;f(x)) مماثلثان بالنسبة لمحور الاراتيب

خاصية

منحنى دالة زوجية مماثل بالنسبة لمحور الاراتيب

تمرين tp

نعتبر الدالة العددية المعرفة كالتالي

f(x)=	1
	x²-2

1) حدد مجموعة تعريف الدال
2) بين ان الدالة زوجية

تصحيح

1) هذه الدالة معرفة اذا كان مقامها غير منعدم
x²-2≠0⇔ x²-2=0 ⇔ ⇔ x=√2 ∨ x=-√2
اذن D=IR\{-√2; √2}

2) نبين ان الدالة زوجية
مجموعة التعريف ممركزة لان
-√2 ; √2, لا ينتميان الى مجموعة التعريف
لدينا ∀x∈D, (-x)∈D
ليكن x∈D

f(-x)=	1	=	1
	(-x)²-2		x²-2

يعني f(-x)=f(x)
اذن الدالة f زوجية

1.1.2. تعريف الدالة الفردية

نقول ان دالة زوجية اذا تحققت الشروط التالية
أ- مجموعة تعريفها مماثلة بالنسبة ل 0
x∈D, -x ∈D
ب- لكل عنصر من مجموعة التعريف ومقابله لهما نفس الصورة
∀x∈D, f(-x)=-f(x)

مثال

الدالة العددية المعرفة ب
f(x) = x³+2x فردية

ملاحظة

اذا كانت دالة فردية فان كل عنصر من مجموعة التعريف مقابله ايضا موجودا في مجموعة التعريف
لكل عنصر من مجموعة التعريف ومقابله لهما صورتين متقابلتين بالدالة
اذا كانت دالة معرفة على مجموعة غير مماثلة بالنسبة ل 0 فان هذه الدالة ليست فردية.

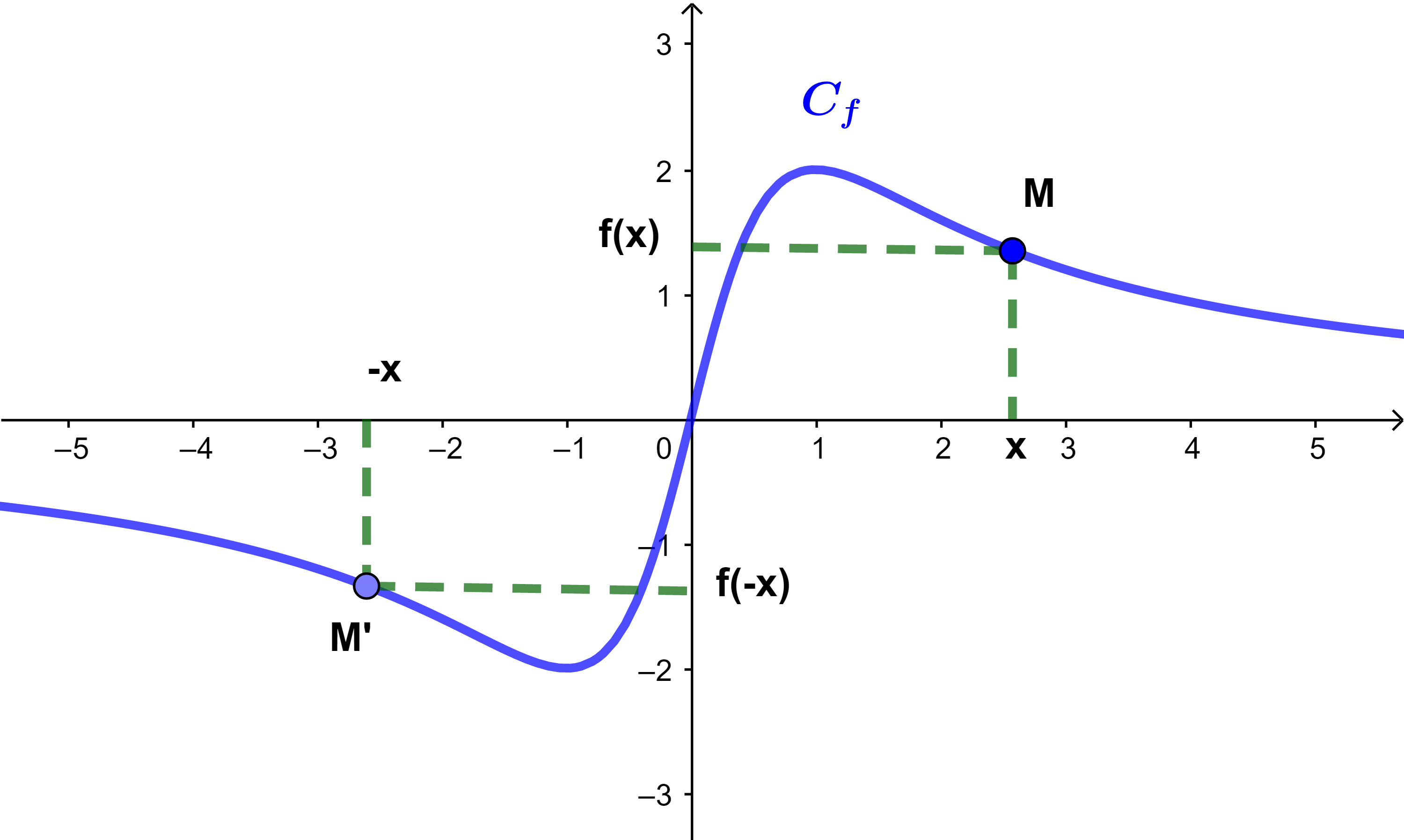
التمثيل المبياني

لتكن f دالة فردية و C_f منحناها في معلم متعامد ممنظم (O;i^→;j^→).
x∈IR, f(-x)=-f(x)⇒: M(x;f(x)) ; M'(-x;-f(x)) مماثلثان بالنسبة لاصل المعلم

تمرين tp

نعتبر دالة عددية معرفة كما يلي
f(x)=x³-3x
بين ان هذه الدالة فردية

تصحيح

لكل x∈IR لدينا x³-3x∈IR
اذن مجموعة تعريف الدالة هي
D_f=IR
∀x∈IR لدينا -x ∈IR.
f(-x)=(-x)³-3(-x)
=-x³+3x,(-x)³=-x³
f(-x)=-x³+3x=-(x³-3x)=-f(x) وهذا يعني ان f دالة فردية

تمرين tp

نعتبر h دالة معرفة ب h(x)=x²+x+3.
ادرس زوجية هذه الدالة

تصحيح

∀x∈IR, x²;x+3∈IR
اذن مجموعة تعريف الدالة هي D_f=IR
لدينا ∀x∈IR; -x ∈IR.
f(-x)=(-x)²+(-x)+3=x²-x+3
f(-x)≠f(x) و f(-x)≠-f(x) وهذا يعني ان الدالة ليست زوجية وليست فردية

تمرين tp

نعتبر الدالة العددية المعرفة كما يلي

f(x)=	2x
	x²-2

أ- حدد مجموعة تعريفها
ب- بين ان هذه الدالة فردية

1.1.3 تعريف الدالة الدورية

f دالة دورية دورها T اذا كان :
1. ∀x ∈D, x+T ; x-T ∈D
2. ∀x ∈D , f(x+T)=f(x)

1.2 الدالة المحدودة

لتكن f دالة عددية معرفة على مجال I

1.2.1 الدالة المكبورة

نقول ان دالة f مكبورة على I اذا تحقق ما يلي:
∃M∈R ; ∀x∈I : f(x) ≤ M

1.2.2 الدالة المصغورة

نقول ان دالة f مصغورة على I اذا تحقق ما يلي:
∃m∈R ; ∀x∈I : f(x) ≥ m

1.2.3 الدالة المحدودة

f دالة محدودة على I اذا تحقق ما يلي
∃m و M∈R ; ∀x∈I : m≤f(x)≤M
او ايضا
f محدودة على I ⇔ ∃α> 0 ; ∀x∈I: |f(x)|≤α.

تمرين tp

f دالة عددية معرفة كما يلي

f(x)=	sinx
	x²+1

بين ان الدالة f محدودة