1.3 مقارنة دالتين

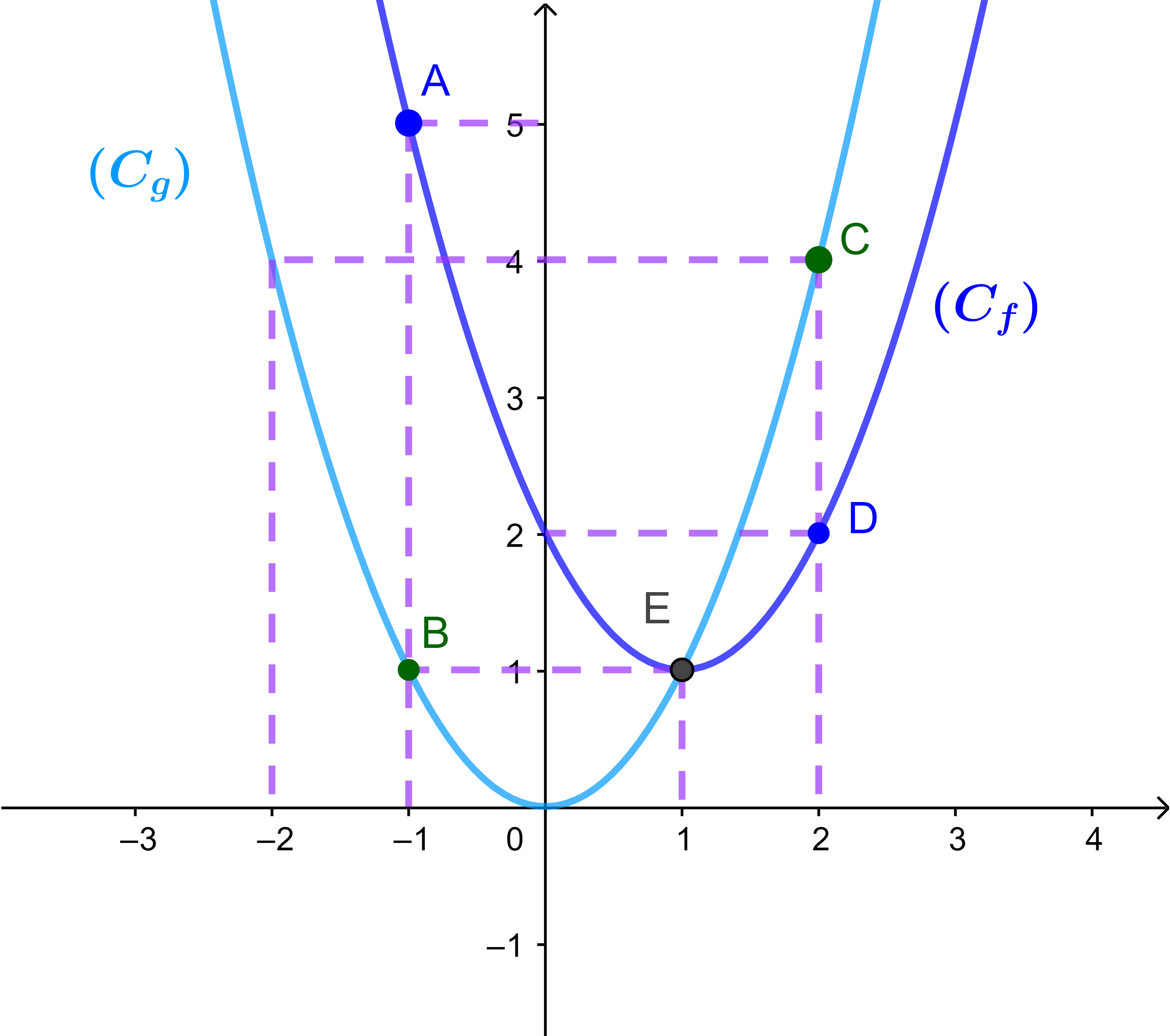
1.3.1 مثال

لتكن f و g دالتين معرفتين كالتالي
f(x)=x²-2x+1 و g(x) =x²
انشئ كل من المنحنى C_f و C_g
قارن مبيانيا وجبريا بين f و g

1.3.2 تعريف 1

نقول ان f و g متساويتان ونكتب f=g اذا تحقق ما يلي
1) D_f = D_g
2) ∀x∈D : f(x)=g(x)

1.3.3 تعريف 2

f < g على I⊂D اذا كان ∀x∈I: f(x) < g(x)
مبيانيا: f < g يعني C_f تحت C_g على I

1.4 مطارف دالة عددية

1.4.1 تعريف القيمة الدنيا لدالة عددية

f دالة عددية معرفة على مجال I, (I⊂D), القيمة الدنيا لدالة عددية f على المجال I, اصغر قيمة لصور عناصر المجال I بواسطة الدالة f. وبتعبير آخر
m قيمة دنيا ل f على I اذا وجد عدد حقيقي a في المجال I بحيث x∈I: f(x)≥m=f(a)

مثال

f دالة عددية معرفة كما يلي f(x)=x²+1, بين ان 1 قيمة دنيا للدالة f

تصحيح

لدينا لكل x∈IR, x²≥0 اذن x²+1≥1
ومنه فان لكل x∈IR, f(x)≥1
يبقى معرفة هل يوجد عنصر a من I=IR بحيث f(a)=1, يكفي حل المعادلة f(x)=1 في المجال I
f(x)=1 يعني x²+1=1 يعني x²=0 اي x=0 اذن 1=f(0) قيمة دنيا ل f "واصلة في 0 "

1.4.2 تعريف القيمة القصوى لدالة عددية

f دالة عددية معرفة على مجال I, (I⊂D), القيمة القصوى لدالة عددية f على المجال I, اكبر قيمة لصور عناصر المجال I بواسطة الدالة f. وبتعبير آخر
M قيمة قصوى ل f على I اذا وجد عدد حقيقي a في المجال I بحيث x∈I: f(x)≤M=f(a)

مثال

f دالة عددية معرفة كما يلي f(x)=-x²+3, بين ان 3 قيمة قصوى للدالة f

تصحيح

لدينا لكل x∈IR, -x²≤0 اذن -x²+1≤3
ومنه فان لكل x∈IR, f(x)≤3
يبقى معرفة هل يوجد عنصر a من I=IR بحيث f(a)=3, يكفي حل المعادلة f(x)=3 في المجال I
f(x)=3 يعني -x²+3=3 يعني x²=0 اي x=0 اذن 3=f(0) قيمة قصوى ل f "واصلة في 0 "

1.4.3 تعريف مطارف دالة عددية

مطراف دالة عددية على مجال I, هو كل قيمة قصوى او قيمة دنيا للدالة f على المجال I

مثال

f دالة عددية معرفة كما يلي : f(x)=2x²+4x+5 بين ان 3 هو مطراف للدالة f على IR.

تصحيح

لدينا لكل x∈IR, f(x)-3=2x²+4x+5-3=
2x²+4x+2 =2(x²+2x+1) =2(x+1)² موجب اذن لكل x∈IR لدينا f(x)≥3,
الآن يجب معرفة هل يوجد عنصر a من المجال I بحيث f(a)=3.
f(a)=3 يعني f(a)-3=0
اي 2(a+1)²=0
اي a=-1 اذن 3=f(-1) هي قيمة دنوية للدالة f
اذن 3 مطراف للدالة f واصلة عند -1 على IR.

1.5 الدالة الرتيبة

1.5.1 تعاريف:

f دالة معرفة على I
1) f تزايدية على I اذا:
∀x;y ∈I: x < y⇒f(x)≤f(y)
2) f تزايدية قطعا على I اذا:
∀ x ; y ∈ I : x < y ⇒ f(x) < f(y)
3) f تناقصية على I اذا:
∀ x ; y ∈ I : x < y ⇒f(x) ≥ f(y)

4) f تناقصية قطعا على I اذا
∀ x ; y ∈ I : x < y ⇒f(x) > f(y)
5) f تابثة على I اذا:
∀x;y∈I: x < y ⇒f(x)=f(y)

تعريف

نقول ان دالة رتيبة على مجال I, اذا كانت اما تزايدية على I واما تناقصية على I.

مثال 1

f دالة عددية معرفة كما يلي : f(x)=x³ ادرس رتابة الدالة f على المجموعة IR

تصحيح

لكل x∈IR; x³∈IR اذن D=IR
x; y∈IR بحيث x< y
بما ان الاس 3 فردي فان المتفاوتة لا تتغير اذن x³< y³ او f(x) < f(y)
ومنه فان f تزايدية قطعا على IR وبالتالي f رتيبة قطعا على IR

مثال 2

f دالة عددية معرفة كما يلي f(x)=x² ادرس رتابة الدالة f على IR+ ثم على IR- .

التصحيح
لكل x∈IR; x²∈IR اذن D=IR
1) ليكن x; y∈IR+ بحيث x< y.
بما ان x و y موجبان معا فان المتفاوتة لا تتغير اذن x²< y² او f(x)< f(y)
وبالتالي f تزايدية قطعا على IR+
2) ليكن x; y∈IR+ بحيث x< y.
بما ان x و y سالبان معا والاس 2 زوجي فان المتفاوتة تتفير اذن x²> y² او f(x)> f(y)
ومنه قان f تناقصية قطعا على IR- وبالتالي f ليست رتيبة على IR

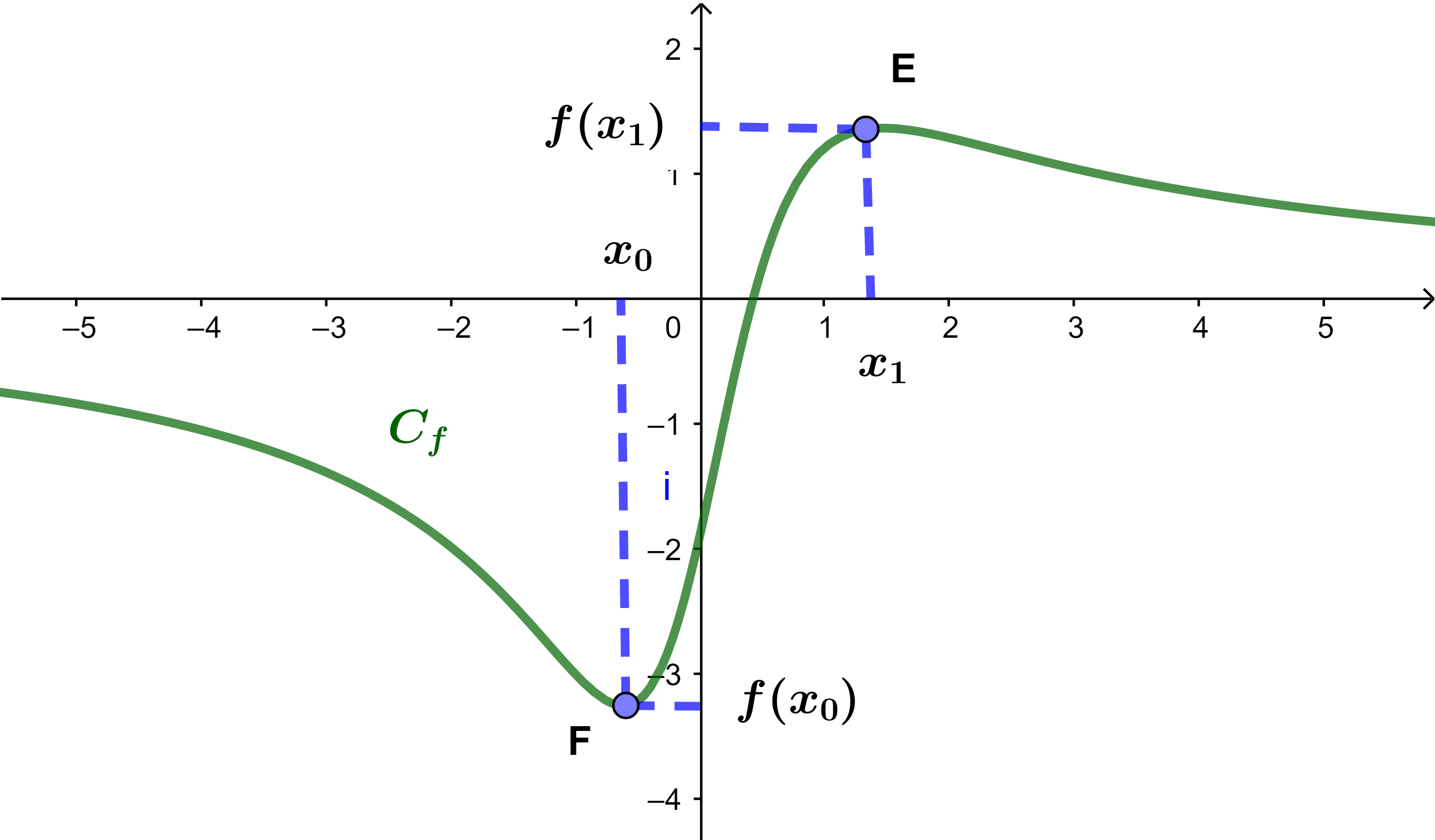
1.5.2 التأويل المبياني

f دالة عددية و (C) منحناها انظر الشكل اسفله
1) f تزايدية على ]-∞;x₀]
2) f تابتة على [x₀;x₁]
3) f تناقصية على [x₁;+∞[

جدول تغيرات f