تمرين 8 tp

ليكن x ;y∈IR
بين ان (x≠y ∧ x+y≠2) ⇒ x²-2x≠y²-2y

تصحيح

يكفي ان نبين ان x²-2x=y²-2y⇒x=y ∨ x+y=2
x²-2x=y²-2y⇒x²-2x+1=y²-2y+1
⇒(x-1)²=(y-1)²
⇒x-1=y-1 ∨ x-1=-(y-1)
⇒x=y ∨ x+y=2
اذن x²-2x=y²-2y⇒x=y ∨ x+y=2
ومنه فان x≠y ∧ x+y≠2 ⇒ x²-2x≠y²-2y صحيحة

تمرين 9 tp

بين بفصل الحالات
∀n∈IN: 3 | n(n+1)(n+2)

تصحيح

اذا n=3k, k∈IN فان 3|3k(3k+1)(3m+2)
اذا n=3k+1, k∈IN فان
n(n+1)(n+2)=(3k+1)(3k+2)(3k+3)
=3(3k+1)(3k+2)(k+1)
لدينا 3|3 اذن 3|n(n+1)(n+2)

اذا n=3k+2, k∈IN فان
n(n+1)(n+2)=(3k+2)(3k+3)(3k+4)
=3(3k+2)(k+1)(3k+4)
لدينا 3|3 اذن 3|n(n+1)(n+2)
وبالتالي
∀n∈IN: 3|n(n+1)(n+2)

تمرين 10 tp

ليكن a∈IR
بين ان (∀ε>0; |a|<ε) ⇒ a=0

تصحيح

يمكن استعمال الاستدلال بمضاد للعكس
يعني نبين
a≠0 ⇒ ∃ε>0; |a|≥ε
اذن اذا a≠0 يكفي اخذ

|a|≥	1	|a| لان	ε=	1	|a|
	2			2

ومنه فان
a≠0 ⇒ (∃ε>0; |a|≥ε)
وبالتالي
(∀ε>0; |a|<ε) ⇒ a=0

تمرين 11 tp

ليكن x;y∈IR+ بين ان الستلزام التالي
(x+y+2=2(√(x)+√(y)))⇒ x=y=1

تصحيح

(x+y+2=2(√(x)+√(y)))
⇒[x+2√(x)+1]+[y-2√(y)+1]=0
⇒[(√x)²-2√(x)+1²]+[(√y)²-2√(y)+1²]=0
⇒(√(x) -1)²+[(√(y)-1)²=0
⇒√(x)-1=0 ∧ √(y)-1=0
⇒√(x)=1 ∧ √(y)=1
√√(x)²=1 ∧ √(y)²=1 ⇒x=1 ∧ y=1

تمرين 12 tp

ليكن x;y;z∈IR
بين ان النظمة التالية ليس لها حل

{	x-z>1
	y-x> 1
	y-z≤2

تصحيح

نستعمل الاستدلال بالخلف نفترض ان النظمة لها حل نرمز له ب (a;b;c)
اذن a-c>1 ⇔ a>1+c

⇔ -a< -1-c
⇔ b-a< -1-c+b
⇔ b-a< -1+(b-c)
وحسب المعادلة (3) لدينا b-c≤ 2 اي -1+(b-c)≤ 2-1
اي b-a< 1 وهذا يتناقض مع النظمة (2)
اذن ما افترضناه كان خاطئا وبالتالي النظمة ليس لها حل

تمرين 13 tp

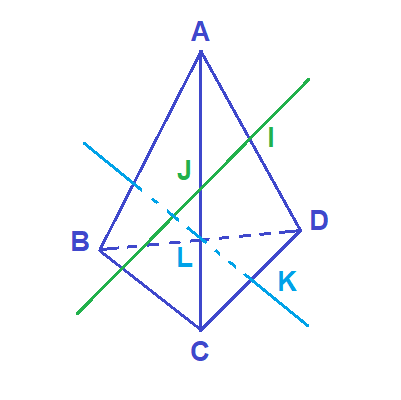
ليكن ABCD رباعي اوجه و I;J;L;K منتصفات القطع [AD]; [AC]; [BD]; [CD] على التوالي
بين ان المستقيمين (IJ) و (KL) منفصلان

تصحيح

نفترض ان (IJ) و (KL) متقاطعان في نقطة O
لدينا O∈(IJ)⊂(ACD)
وايضا O∈(KL)⊂(BCD)
اذن O∈(ACD)∩(BCD)=(CD) ومنه فان O∈(CD) اذن (IJ) يقطع المستقيم (CD) وهذا يتناقض مع خاصية منتصفات مثلث
وبالتالي (IJ) و (KL) منفصلان