الجداء السلمي (3)
تمرين 13 tp
ليكن (D) مستقيما معادلته x-2y+2=0
1) تحقق ان النقطة A(0;1)∈(D)
2) حدد معادلتي الدائرتين المماستين للمستقيم (D) عند النقطة A وشعاعهما √(5)
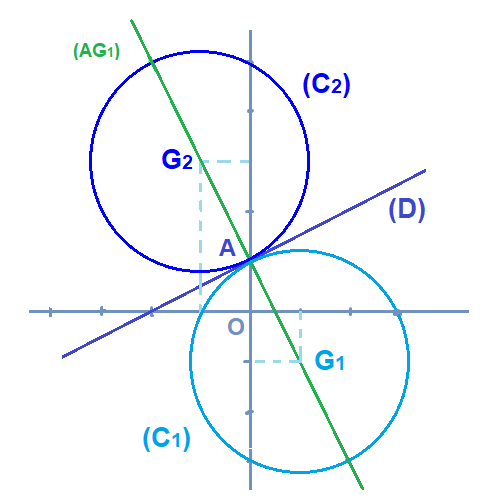
3) انشئ الشكل
تصحيح
1) 0-2.1+2=-2+2=0 ⇒ A∈(D)
2) نرمز لاحدى الدائرتين ب (C1) ومركزها G1(x;y)
ولدينا (AG1)⊥(D) اذن جداء ميلهما mm1=-1⇒m1=-2<
AG1=√(5)⇔ (x-0)²+(y-1)²=5
⇔x²+y²-2y-4=0 , (1)
نحدد معادلة المستقيم (AG1)
(AG1): y=-2x+p وبما ان A∈(AG1) فان
1=-2.0+p⇒ p=1
(AG1): 2x+y-1=0 , (2)
اذن الزوج (x;y) يحقق النظمة التالية
| { | x²+y²-2y-4=0 |
| 2x+y-1=0 | |
| ⇒ { | x²+(1-2x)²-2(1-2x)-4=0 |
| y=1-2x | |
| ⇒ { | 5x²=5 |
| y=1-2x |
| ⇒ { | x=1 ∨ x=-1 |
| y=1-2x |
| ⇒ { | x=1 ∧ y=-1 |
| ∨ x=-1 ∧ y=3 |
والثانية (C2) مركزها G2(-1;3) وشعاعها √(5)
3)
تمرين 14 tp
لتكن (C) دائرة مركزها G(2;-1) شعاعها √(2) و E(5;0) نقطة من المستوى
1) (q1) حدد معادلة ديكارتية للدائرة (C)
(q2) تحقق ان E خارج الدائرة (C)
2) انشئ الدائر (C)
3) حدد معادلتي المماسين للدائرة (C) والمارين من النقطة E
تصحيح
1) (q1) M(x;y)∈(C) ⇔ GM=√(2)
⇔ (x-2)²+(y+1)²=2
⇔ x²+y²-4x+2y+3=0
(C): x²+y²-4x+2y+3=0
(q2) E(5;0)∈ext(C) , 5²-20+3=8>0
2)
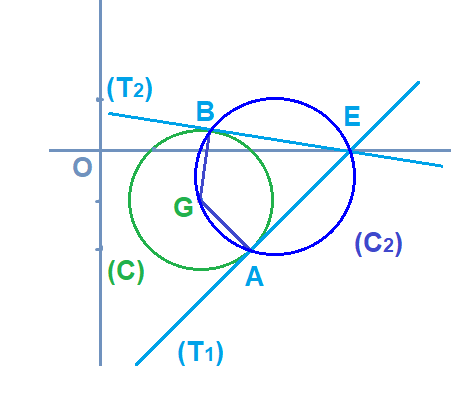 3) نرمز لاحد المماسين ب (T1) عند النقطة A(x;y)
3) نرمز لاحد المماسين ب (T1) عند النقطة A(x;y)
لدينا (GA)⊥(T1) اذن
EA→.GA→=0
⇔ (x-2)(x-5)+(y+1)y=0
⇔ x²+y²-7x+y+10=0 , (1)
وهذا يعني ان النقطة A تنتمي الى الدائرة (C2) التي مركزها
I(3,5 ; -0,5) بالاضافة الى الدائرة (C)
اذن زوج احداثيتي A يحقق النظمة التالية
| { | x²+y²-4x+2y+3=0 , (1) |
| x²+y²-7x+y+10=0 , (2) |
x²+(-3x+7)²-4x+2(-3x+7)+3=0
⇔ 5x²-26x+33=0
نحل هذه المعادلة Δ=16 >0
| x1= | 22 | = | 11 |
| 10 | 5 | ||
| x2= | 30 | = 3 | |
| 10 |
(i1) x=3⇒ y=-9+7=-2
(T1) مماس للدائرة (C1) عند النقطة A(3 ; -2)
نحدد معادلة (T1)=(EA)
M(x;y)∈(T1)⇔ det(EM;EA)=0
(x-5).(-2)-(y-0).(-2)=0
⇔ -2x+2y+10=0
(T1): x-y-5=0
(i2) لدينا
| x= | 11 | ⇒ | y= | 2 |
| 5 | 5 |
| B( | 11 | ; | 2 | ) |
| 5 | 5 |
M(x;y)∈(T1)⇔ det(EM;EB)=0
| (x-5) | 2 | -(y-0). | -14 | = 0 | |
| 5 | 5 | ||||
| 2 | x + | 14 | y - | 10 | = 0 |
| 5 | 5 | 5 |
تمرين 15 tp
حدد تمثيلا بارامتريا للدائرة التي مركزها I(-2 ; 5) وشعاعها R=3
تصحيح
تمثيل بارامتري للدائرة C التي مركزها I(-2 ; 5) وشعاعها R=3 هي النظمة التالية
| { | x = -2 + 3cosθ | ; θ∈IR |
| y = 5 + 3sinθ |