الجداء السلمي (2)
تمرين 11 tp
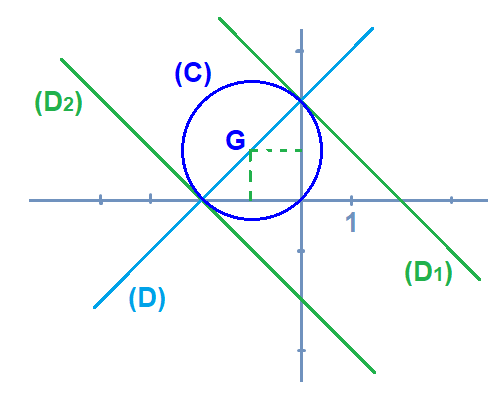
لتكن (C) دائرة معادلتها x²+y²+4x+2y+1=0
1) حدد مركز وشعاع الدائرة (C)
2) حدد تمثيلا بارمتريا لمستقيم (D)
معادلته x+y+1=0
3) انشئ الشكل
4) بين ان المستقيم (D) يقطع الدائرة في نقطتين ينبغي تحديدهما.
تصحيح
1) لدينا x²+y²+4x+2y+1=0 ⇔
(x²+2.2x+2²)-2²+(y²+2.1y+1²)-1²+1=0
⇔ (x+2)²+(y+1)²=4=2²
اذن (C) دائرة مركزها G(-2;-1) وشعاعها 2
2) نحدد تمثيلا بارمتريا للمستقيم (D)
M(x;y)∈(D)⇔ ∃t∈IR: AM→=tu→
| ⇔{ | x= 2-t | ; t∈IR |
| y=-3 + t |
هذه النظمة هي تمثيل بارامتري للمستقيم (D)
3)
4) نبين ان المستقيم (D) يقطع الدائرة في نقطتين
لذلك نحسب d(G;(D))
| d(G;(D)) = | |-2-1+1| | = √(2) < 2 |
| √(2) |
اذن (D) يقطع الدائرة في نقطتين A ; B
نحل النطمة التالية
| x²+y²+4x+2y+1=0 | ; t∈IR | |
| x= 2-t | ||
| y=-3 + t |
(2-t)²+(-3+t)²+4(2-t)+2(-3+t)+1=0
⇔ 2t²-12t+16=0
⇔ t1=2 ; t2=4
t1=2⇒ x=2-2=0 ; y=-3+2=-1
نحصل على النقطة الاولى نرمز لها ب A(0;-1)
t2=4⇒ x= 2-4=-2 ; y=-3+4=1
نحصل على النقطة الثانية نرمز لها ب B(-2;1)
تمرين 12 tp
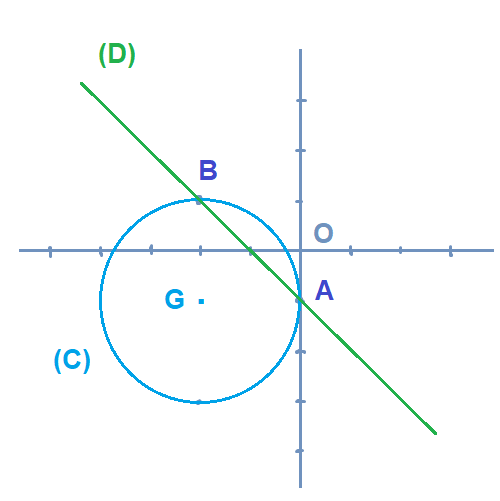
ليكن (D1) مستقيما معادلته
x+y-2=0
1) (q1) تحقق ان A(0;2)∈(D1)
(q2) حدد معادلة المستقيم (D) المار من A والعمودي على (D1)
2) ليكن (D2) مستقيما معادلته
x+y+2=0
(q1) حدد B نقطة تقاطع (D) و (D2)
(q2) حدد d(A;(D2))
3) حدد الدائرة المماسة لكل من (D1) و (D2) عند النقطتين
A و B على التوالي
4) انشئ الشكل
تصحيح
1) (q1) (D1): x+y-2=0
0+2-2= 0 ⇒ A∈(D1)
(q2) بما ان (D)⊥(D1) فان جداء ميلهما m.m1=-1
⇒ (D): y=x+p
بما ان A∈(D) فان
2=0+p اي p=2 ومنه فان (D): y=x+2
(D): x-y+2=0
2) (q1) B نقطة تقاطع (D) و (D2)
نحل النظمة التالية
| { | x-y+2=0 |
| x+y+2=0 |
| { | x-y+2=0 | ⇔ { | y=x+2 |
| x+y+2=0 | 2x+4=0 | ||
| ⇔ | { | y=-2+2=0 | |
| x=-2 |
اذن (D)∩(D2)={B(-2;0)}
(q2) نحدد d(A;(D2))
| d(A;(D2)) = | |0+2+2| | = | 4 | =2√(2) |
| √(1²+1²) | √(2) |
3) نحدد الدائرة المماسة لكل من (D1) و (D2) عند النقطتين
A و B على التوالي
بما ان (َAB)⊥(D1) ; (AB)⊥(D2) فان القطعة [AB] قطر للدائرة (C)
ومنتصفها هو مزكز الدائرة وشعاعها نصف طول القطعة
| xG = | 0+(-2) | = -1 ; | yG = | 2+0 | = 1 |
| 2 | 2 |
وبالتالي الدائرة مركزها G(-1;1) وشعاعها R=AB÷2=√2
4) الشكل