Produit scalaire (3)
Exercice 1 tp
Le plan ℙ est rapporté à un repère orthonormé
(O;i→;j→). On considère dans ℙ une droite (D1) d'équation
x+y-2=0.
1) (a) Vérifier que A(0;2)∈(D1).
(b) Déterminer une équation de la droite (D) passant par A et perpendiculaire à (D1).
2) Soit (D2) une droite d'équation
x+y+2=0.
(a) Déterminer B point de rencontre entre (D) et (D2).
(b) Déterminer d(A;(D2)).
3) Déterminer le cercle tangent à (D1) et à (D2) respectif en
A et B.
4) Tracer la figure .
Correction
1) (a) (D1): x+y-2=0
0+2-2= 0 ⇒ A∈(D1).
(b) puisque (D)⊥(D1) alors m.m1=-1
⇒ (D): y=x+p
puisque A∈(D) alors
2=0+p ou encore p=2 ainsi (D): y=x+2
(D): x-y+2=0.
2) (a) B est le point de rencontre de (D) et (D2)
on résout le système suivant
| { | x-y+2=0 | ⇒ { | y=x+2 |
| x+y+2=0 | 2x+4=0 |
| ⇒{ | y=-2+2=0 |
| x=-2 |
(D)∩(D2)={B(-2;0)}.
(b) On calcule d(A;(D2))
| d(A;(D2)) = | |0+2+2| | = | 4 | = 2√(2) |
| √(1²+1²) | √(2) |
3) Le cercle de sorte que (D1) et (D2) lui soient tangentes respectives en
A et B
puisque (َAB)⊥(D1) et (AB)⊥(D2) alors le segment [AB] est un diagonal au cercle (C)
son milieu est le centre du cercle
et la moitié de la longueur du segment est le rayon du cercle.
| { | xG = | 0+(-2) | = -1 |
| 2 | |||
| yG = | 2+0 | = 1 | |
| 2 |
G(-1;1) et
R=AB÷2=√2
et donc le cercle est de centre G(-1;1) et de rayon √(2).
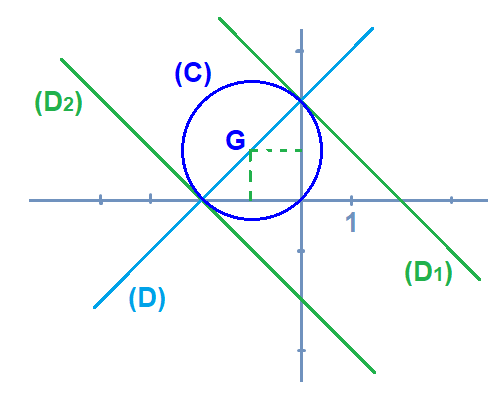
4) La figure