Produit scalaire (4)
Exercice 1 tp
Le plan ℙ est rapporté à un repère orthonormé
(O;i→;j→). On considère dans ℙ
deux points A(2;-1) et B(4;1).
Déterminer une équation cartésienne d'un cercle de sorte que [AB] est l'un de ses diamètres.
Exercice 2 tp
Le plan ℙ est rapporté à un repère orthonormé
(O;i→;j→). On considère dans ℙ
trois points E(-1;-1); F(-3;1) et G(2;2).
1) Vérifier que E ; F و G ne sont pas alignés.
2) Vérifier que G'(-2;0) est milieu du segment [EF].
3) Montrer que x-y+2=0 est une équation du médiatrice passant par G'.
4) Montrer que x+y-1=0 est une équation du médiatrice du segment [EG].
5) Résoudre le système suivant et déduire une équation cartésienne du cercle (C)
| { |
| x - y + 2 = 0 |
| x + y - 1 = 0 |
Exercice 3 tp
Le plan ℙ est rapporté à un repère orthonormé
(O;i→;j→). On considère dans ℙ
un cercle (C) d'équation x²+y²+4x+2y+1=0.
1) Déterminer le centrez et le rayon de (C).
2) Déterminer une représentation paramétrique de la droite (D)
d'équation x+y+1=0.
3) Tracer la figure.
4) Montrer que (D) coupe le cercle en deux points.
Correction
1) x²+y²+4x+2y+1=0 ⇔
(x²+2.2x+2²)-2²+(y²+2.1y+1²)-1²+1=0
⇔ (x+2)²+(y+1)²=4=2²
donc (C) est un cercle de centre G(-2;-1) et de rayon 2
2) M(x;y)∈(D) ⇔ (∃t∈IR): AM→=tu→
| ⇔{ | x = 2-t | (t∈IR) |
| y = -3 + t |
Ce système est une représentation paramétrique de (D).
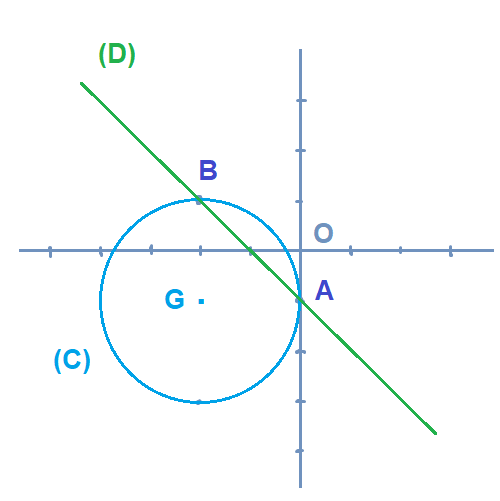
4) On montre que (D) coupe le cercle
pour cela on calcule d(G;(D))
| d(G;(D)) = | |-2-1+1| | = √(2) < 2 |
| √(2) |
donc (D) coupe le cercle en deux points A et B
on résout le système suivant
| x²+y²+4x+2y+1=0 | (t∈IR) | |
| x = 2-t | ||
| y = -3 + t |
(2-t)²+(-3+t)²+4(2-t)+2(-3+t)+1=0
⇔ 2t²-12t+16=0
⇔ t1=2 et t2=4
t1=2 ⇒ x=2-2=0 et y=-3+2=-1
on trouve le premier point A(0;-1)
t2=4 ⇒ x= 2-4=-2 et y=-3+4=1
on trouve le deuxième point B(-2;1).