Produit scalaire (6)
ُExercice 1 tp
Le plan ℙ est rapporté à un repère orthonormé
(O;i→;j→). On considère dans ℙ
une droite (D) d'équation x-2y+2=0.
1) Vérifier que A(0;1)∈(D).
2) Déterminer deux équations pour deux cercles de même rayon √(5) de sorte que la droite (D) leur soit tangente en A.
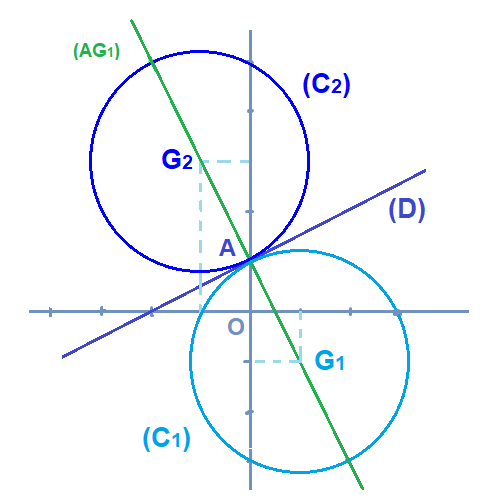
3) Tracer la figure.
Correction
1) 0-2.1+2=-2+2=0 ⇒ A∈(D).
2) On désigne un des deux cercles par (C1) et de centre G1(x;y)
on a (AG1)⊥(D) donc le produit de leurs coéfficients directeurs est mm1=-1⇒m1=-2
AG1=√(5)⇔ (x-0)²+(y-1)²=5
⇔x²+y²-2y-4=0 (1).
On détermine une équation de (AG1).
On a (AG1): y=-2x+p.
Puisque A∈(AG1) alors
1=-2.0+p ⇒ p=1
donc (AG1): 2x+y-1=0 (2)
et donc le couple (x;y) vérifie le système
| { | x²+y²-2y-4 = 0 |
| 2x+y-1 = 0 | |
| ⇒ { | x²+(1-2x)²-2(1-2x)-4=0 |
| y = 1-2x | |
| ⇒ { | 5x² = 5 |
| y = 1-2x |
| ⇒ { | x=1 ∨ x=-1 |
| y=1-2x |
| ⇒ { | x=1 ∧ y=-1 |
| ∨ x=-1 ∧ y=3 |
et donc l'un des cercle de sorte que (D) lui soit tangente en A est (C1) de centre G1(1;-1) et de rayon √(5)
et le deuxième cercle (C2) de centre G2(-1;3) et de rayon √(5).
3)
Exercice 2 tp
Le plan ℙ est rapporté à un repère orthonormé (O;i→;j→). On considère dans ℙ un cercle (C) définie par le représentation paramétrique suivant
| { | x = 1 - cosθ | (θ∈IR) |
| y = 2sinθ |
1) Déterminer le centre et le rayon du cercle (C).
2) Déduire une équation cartésienne du cercle (C).
Exercice 3 tp
Le plan ℙ est rapporté à un repère orthonormé
(O;i→;j→). On considère dans ℙ un cercle (C) de centre I(-2 ; 5) et de rayon R=3.
Déterminer une représentation paramétrique du cercle (C).
Correction
Notons que M(x;y)∈C(I;R) ⇔ IM→=R(cosθi→+sinθj→) tel que θ∈IR.
(C) est un cercle de centre I(-2 ; 5) et de rayon R=3
donc une représentation paramétrique du cercle est le système suivant
| { | x = -2 + 3cosθ | (θ∈IR) |
| y = 5 + 3sinθ |