Produit scalaire (5)
Exercice 1 tp
Le plan ℙ est rapporté à un repère orthonormé
(O;i→;j→). On considère dans ℙ un cercle (C) de centre G(2;-1) et de rayon √(2).
Soit E(5;0) un point du plan.
1) (a) Déterminer une équation du cercle (C).
(b) Vérifier que E est à l'extérieur du cercle (C).
2) Tracer le cercle (C).
3) Déterminer les deux tagentes à (C) passant par E.
Correction
1) (a) M(x;y)∈(C) ⇔ GM=√(2)
⇔ (x-2)²+(y+1)²=2
⇔ x²+y²-4x+2y+3=0
(C): x²+y²-4x+2y+3=0.
(b) E(5;0)∈ext(C) car 5²-20+3=8>0.
2)
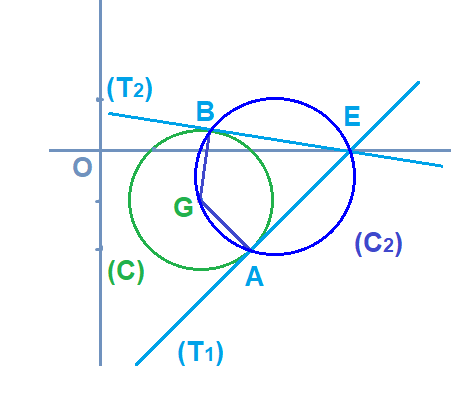
3) On désigne par (T1) l'une des tangentes au point A(x;y)
on a (GA)⊥(T1) donc
EA→.GA→=0
⇔ (x-2)(x-5)+(y+1)y=0
⇔ x²+y²-7x+y+10=0 (1)
et cela signifie que A appartient au cercle (C) et au cercle (C2) de centre
I(3,5 ; -0,5).
Donc le couple des coordonnées de A vérifie le système suivant
| { | x²+y²-4x+2y+3=0 | (1) |
| x²+y²-7x+y+10=0 | (2) |
on fait l'opération
(1)-(2) on obtient donc l'équation
3x+y-7=0.
3x+y-7=0 ⇔ y=-3x+7 (3) on remplace la valeur de y dans
(1) ou (2)
on obtient x²+(-3x+7)²-4x+2(-3x+7)+3=0
ou encore 5x²-26x+33=0.
On résout l'équation
Δ=16 >0
| x1 = | 22 | = | 11 |
| 10 | 5 | ||
| x2 = | 30 | = 3 | |
| 10 |
(a) x=3 ⇒ y=-9+7=-2
(T1) est tangente à (C1) au point A(3 ; -2).
On détermine (T1)=(EA)
M(x;y)∈(T1) ⇔ det(EM→;EA→)=0
⇔ (x-5).(-2)-(y-0).(-2)=0
⇔ -2x+2y+10=0
ainsi (T1): x-y-5=0.
(b) On a
| x= | 11 | ⇒ | y= | 2 |
| 5 | 5 |
(T2) est tangente à (C1) au point B
| B( | 11 | ; | 2 | ) |
| 5 | 5 |
De la même façon on détermine l'équation de (T2)=(EB)
M(x;y)∈(T1)⇔ det(EM→;EB→)=0
| (x-5) | 2 | -(y-0). | -14 | = | 0 | |
| 5 | 5 | |||||
| 2 | x + | 14 | y - | 10 | = | 0 |
| 5 | 5 | 5 |
ainsi (T2): x+7y-5=0.