La rotation dans le plan (3)
Exercice 1 tp
Soient EFGH un carré de centre O ; N∈[FG] tel que FN→=xFG→ et M∈[EF] tel que EM→=xEF→ avec (x∈IR).
1) Tracer la figure.
2) Déterminer le centre et le rayon de la rotation R qui transforme F en E et G en F.
3) Montrer que R(N)=M.
4) Soit I le milieu du segment [EN]
(a) Montrer que IEF est un triangle isocèle.
(b) Déterminer R(I).
5) Déterminer le lieu du point I quand M change sur le segment [EF].
Correction
1)
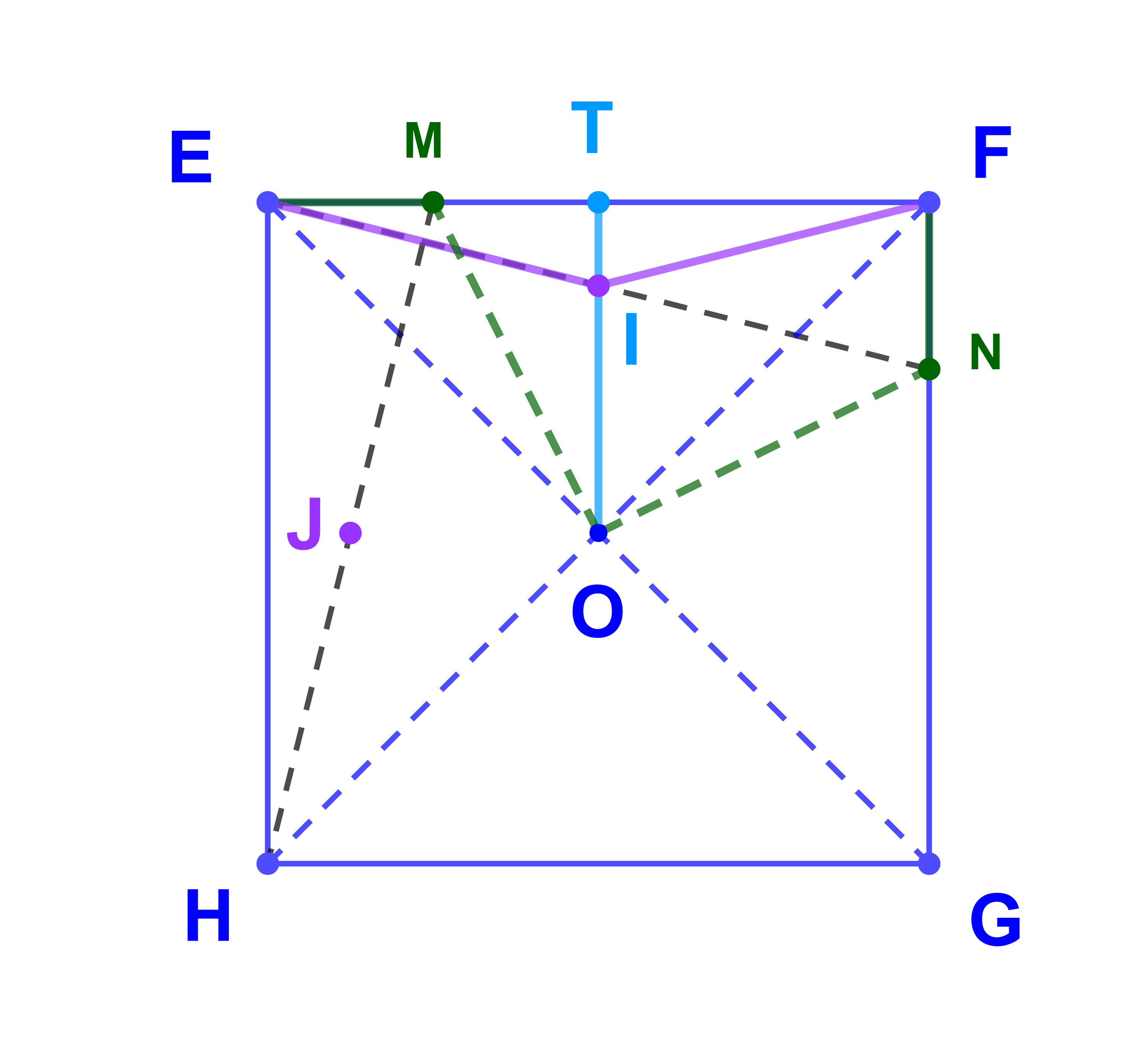
2) R(F)=E⇒Ω∈med(EF)
R(G)=F⇒Ω∈med(FG)
donc
G∈med(EF)∩med(FG)
et puisque EFGH est un carré
alors med(EF)∩med(FG)={O}
ainsi O est le centre de R.
Notons que les diagonales d'un carré sont perpendiculaires
donc
| (OF;OE)≡ | π | [2π] |
| 2 |
Alors R est une rotation de centre O et d'angle
| α≡ | π | [2π] |
| 2 |
3) On montre que R(N)=M et on pose R(N)=N'.
On a FN→=xFG→
Notons que la rotation conserve le coefficient de colinéarité de deux vecteurs.
Et puisque R(F)=E et R(G)=F alors EN'→=xEF→
et on a EM→=xEF→ donc
EN'→=EM→ et cela signifie que N'=M alors
R(N)=M.
4) (a) On considère le triangle EGN.
on a O est milieu de la diagonale [EG] et I est le milieu du segment [EN]
donc (OI)||(GN) et puisque EFGH est un carré alors (OI) est médiatrice du segment [EF]
donc IE=IF ainsi IEF est un triangle isocèle.
(b) On détermine R(I).
On a OE=OH et (OE)⊥(OH) donc R(E)=H.
On a R(N)=M et I est le milieu du segment [EN]
et puisque la rotation conserve le milieu
alors R(I)=J tel que J est le milieu du segment [MH].
5) On a EM→=xEF→
donc quand M change sur le segment [EF] alors le nombre x change dans l'intervalle [0;1].
| IO→ = | 1 | NG→ = | 1 | (NF→+FG→) |
| 2 | 2 |
| = | (1-x) | FG→ = tFG→ (t∈[0; | 1 | ]) |
| 2 | 2 |
et cela signifie que le lieu du point I est le segment [OT].