Etude des fonctions numériques (9)
Exercice 1 tp
Soit f une fonction numérique définie par
f(x) = 2x+√(x²+1)
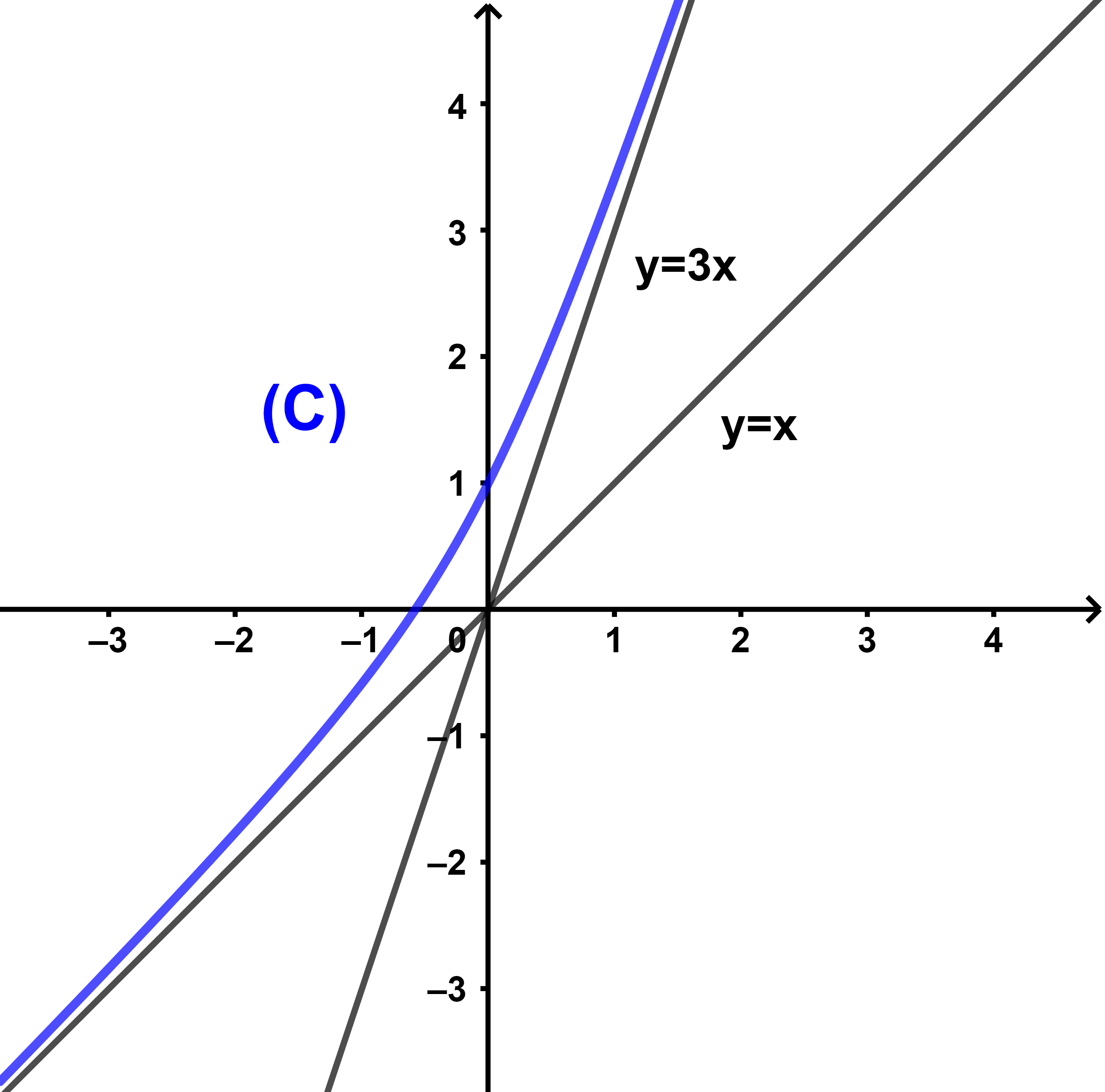
et (C) sa courbe dans un repère orthonormé (O;i→;j→).
1) (a) Calculer les limites suivantes
lim -∞ | f(x) | et | lim +∞ | f(x) |
(b) Montrer que les droites (D): y=3x et (D'): y=x sont deux asymptotes obliques à (C).
2) (a) Montrer que ∀x∈]-∞ ; 0]
x + 2√(x²+1) > 0.
(b) Vérifier que ∀x∈IR
| f '(x) = | x + 2√(x²+1) |
| √(x²+1) |
(c) Déduire la monotonie de f et tracer son tableau de variations.
3) (a) Montrer que l'équation f(x)=0 admet une solution unique α dans l'intervalle I=[-1;0].
(b) Montrer que f admet une fonction réciproque f-1 définie de IR vers IR.
(c) Calculer f(0) et (f-1)'(1).
4) Tracer la courbe (C).
Correction
(a) Limite en - ∞
lim -∞ | f(x) = | lim -∞ | 2x+√(x²(1+ | 1 | )) |
| x² |
√(x²)=|x|
quand x tend vers -∞ x est négatif
ainsi √(x²)=-x.
lim -∞ | f(x)= | lim -∞ | x(2-√(1+ | 1 | )) |
| x² |
Puisque
lim -∞ | √(1+ | 1 | )=1 |
| x² |
| alors | lim -∞ |
f(x)=-∞.(2-1)=-∞ |
(b) Limite en +∞
lim +∞ | f(x)= | lim +∞ | 2x+√(x²+1) |
On a
lim +∞ | 2x = +∞ |
lim +∞ | x²+1 = | lim +∞ | x² = +∞ |
donc
lim +∞ | √(x²+1) =+∞ |
| ainsi | lim +∞ | f(x)= +∞ |
(b) On a
lim +∞ | f(x)= +∞ |
lim +∞ | f(x) - 3x = | lim +∞ | √(x²+1) - x |
| = | lim +∞ |
1 | |
| √(x²+1) + x |
lim +∞ | √(x²+1) = +∞ | lim +∞ | x = +∞ |
| ⇒ | lim +∞ | √(x²+1) + x = +∞ |
| donc | lim +∞ | f(x) - 3x = 0 |
et cela signifie que (D): y=3x est un asymptote oblique à (C) au voisinage de +∞.
On a
lim -∞ | f(x)= -∞ |
lim - ∞ | f(x) - x = | lim - ∞ | √(x²+1) + x |
| = | lim - ∞ |
1 | |
| √(x²+1) - x |
lim -∞ | √(x²+1) = +∞ | lim -∞ | -x = +∞ |
| ⇒ | lim -∞ | √(x²+1) - x = +∞ |
| donc | lim - ∞ | f(x) - x = 0 |
et cela signifie que (D'): y=x est un asymptote oblique à (C) au voisinage de -∞.
2) (a) Soit x∈]-∞ ; 0] donc √(x)=|x|=-x
x²+1>x² ⇒ √(x²+1)>- x
⇒ √(x²+1) + x > 0
ainsi ∀x∈]-∞;0] on a √(x²+1) + x > 0.
(b) La fonction x→x²+1 est strictement positive et dérivable sur IR donc la fonction x⇒√(x²+1) est dérivable sur IR
et on a x→2x est dérivable sur IR donc f est dérivable sur IR.
| f '(x) = 2 + | 2x |
| 2√(x²+1) | |
| = 2 + | x |
| √(x²+1) | |
| = | 2√(x²+1) + x |
| √(x²+1) |
| Alors f '(x) = | x + 2√(x²+1) |
| √(x²+1) |
(c) (∀x∈]-∞;0]) on a √(x²+1) + x>0
et √(x²+1) > 0 donc 2√(x²+1) + x > 0
ainsi (∀x∈]-∞;0]) on a f '(x) > 0.
Soit (x∈]0 ; +∞[) donc x>0 et √(x²+1)>0
et donc f'(x) > 0
alors (∀x∈IR) on a f'(x)>0 et cela signifie que f est strictement croissante sur IR.
(c) Tableau de variations
| x | -∞ | +∞ | |
| f'(x) | + | ||
| f | -∞ | ↗ | +∞ |
3) (a) L'équation f(x)=0.
La fonction f est dérivable sur IR donc dérivable sur l'intervalle I et donc continue sur I.
La fonction f est strictement croissante sur IR en particulier sur I.
f(-1)=2.(-1) + √((-1)²+1)=-2+√(2) < 0
et f(0)=2.0 + √(0²+1)=0+1 > 0.
En utilisant le Théorème des valeurs intermédiaires on déduit que l'équation f(x)=0 admet une solution unique α dans I.
(b) La fonction f est continue et strictement croissante sur IR donc admet une fonction réciproque, notée f-1 définie de f(IR) vers IR
| f(IR)=] | lim -∞ |
f(x) ; | lim +∞ |
f(x)[ |
donc f(IR) = IR.
(c) f(0) = 2.0+√(0²+1) = 1
f(0)=1 ⇔ f-1(1)=0.
On a f est dérivable sur IR donc dérivable au point 0
f'(0)=2≠0 donc f-1 est dérivable au point 1 et on a de plus
| (f-1) '(1) = | 1 | = | 1 |
| f'(0) | 2 |