حساب التكامل (1)
1- تكامل دالة متصلة على قطعة
1.1 تعريف وترميز
لتكن f دالة معرفة على المجال I=[a;b] و F دالة اصلية للدالة f, العدد F(b)-F(a) يسمى تكامل الدالة f من a الى b ويكتب على الشكل التالي
| b ∫ a | f(x)dx | = [F(x)] | b a |
وتقرأ مجموع f(x)dx من a الى b او تكامل من a الى b ل f(x)dx
ملاحظة :
اذا كانت G دالة اصلية اخرى للدالة f فان :
| b ∫ a | f(x)dx | = [G(x)] | b a | = G(b)-G(a)=F(b)-F(a) |
| b ∫ a | f(x)dx = | b ∫ a | f(t)dt | = [F(t)] | b a |
مثال 1
| 2 ∫ 1 | 3x²dx | =[x³] | 2 1 | =8 -1=7 |
مثال 2
| e ∫( 2 | 1 | )dx = [lnx] | e 2 | = lne -ln2= 1-ln2 |
| x |
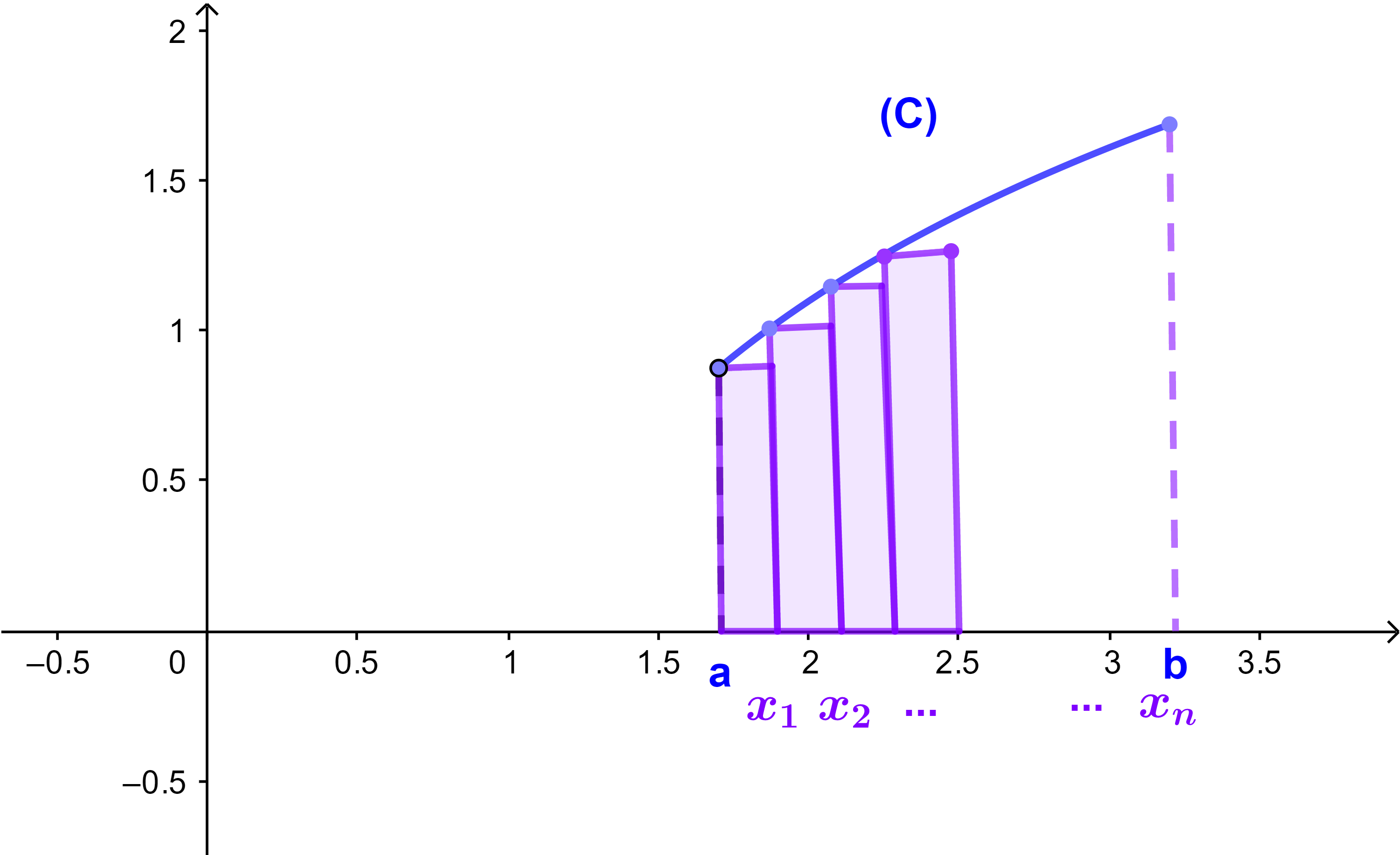
1.2 التأويل الهندسي للعدد
| I= | b ∫ a | f(x)dx |
نقوم بتقسيم القطعة [a;b] الى n قسمة متساوية طولها :
| Δxi= | b-a |
| n |
ونعتبر المستطيلات الصغيرة جدا طولها Δxi وارتفاعها f(xi)
مساحة كل مستطيل تقريبا يساوي Δxi.f(xi)
اي S ≃x1.f(x1) + x2.f(x2) + ... + xn.f(xn)
وعندما n→+∞ فان هذا المجموع يؤول الى S
1.3 خاصيات التكامل
لتكن f و g دالتين متصلتين على I=[a;b] و c∈I و k∈IR
الدالة G المعرفة على I ب :
| x→G(x) = | x ∫ a | f(t)dt |
2- التكامل والعمليات
| b ∫ a | f(x)dx = - | a ∫ b | f(x)dx |
| a ∫ a | f(x)dx = 0 |
| b ∫ a | f(x)dx | = | c ∫ a | f(x)dx + | b ∫ c | f(x)dx |
b ∫ a | (f(x)+g(x))dx = |
| b ∫ a |
f(x)dx + | b ∫ a |
g(x)dx |
| b ∫ a | kf(x)dx | = k | b ∫ a | f(x)dx |
مثال
| 2 ∫ -1 | |x-1|dx = | 1 ∫ -1 | -(x-1)dx + | 2 ∫ 1 | (x-1)dx |
| = [(-1/2)x²+x] | 1 -1 | + [(1/2)x²-x] | 2 1 | =5/2 |
3- التكامل والترتيب
3.1 خاصيات
لتكن f دالة متصلة على المجال I=[a;b],
اذا كانت f موجبة على المجال I فان F' موجبة
اذن F تزايدية على I
ومنه فان F(b)-F(a) موجب
3.1.1 خاصية 1
لتكن f دالة متصلة على المجال I=[a;b], اذا كانت f موجبة على المجال I فان :
| b ∫ a | f(x)dx ≥ 0 |
3.1.2 خاصية 2
لتكن f دالة متصلة على I=[a;b], اذا كانت f سالبة فان :
| b ∫ a | f(x)dx ≤ 0 |
3.1.3 خاصية 2
لتكن f و g دالتين معرفتين على I=[a;b]
اذا كانت f≤g على I فان:
| b ∫ a | f(x)dx ≤ | b ∫ a | g(x)dx |
3.1.4 نتيجة
| | | b ∫ a | f(x)dx | | | ≤ | b ∫ a | |f(x)|dx |
3.2 القيمة الوسيطة
لتكن f دالة متصلة على I=[a;b] و m قيمتها الدنيا و M قيمتها القصوى
لدينا ∀x∈I: m ≤ f(x)≤M اذن :
| m(b-a) ≤ | b ∫ a | f(x)dx ≤ | M(b-a) |
| m ≤ | 1 | b ∫ a | f(x)dx ≤ M |
| b-a |
| f(c)= | 1 | b ∫ a | f(x)dx |
| b-a |
بالتعريف العدد f(c) يسمى القيمة الوسيطة للدالة f على I
تمرين
لتكن f و g و h دوال معرفة على I=[0;1] كما يلي :
f(x)=(1+x²)-1 و g(x)=-0,5x+1 و h(x)=-0,5x²+1
1) بين ان ∀x∈I: g(x)≤f(x)≤h(x)
2) استنتج تأطيرا للعدد:
| 1 ∫ 0 | f(x)dx |