حساب التكامل (3)
5- حساب المساحات والحجوم
5.1 حساب المساحات
5.1.1 Iتقديم
وحدة قياس المساحة ;UA هي مساحة المستطيل OIKJ حيث i→=OI→ و j→=OJ→
نرمز ب S للمساحة المحصورة بين المنحنى Cf ومحور الافاصيل والمستقيمين (D): x=a و (D'): x=b
اذا كانت f تابتة اي f=k فان
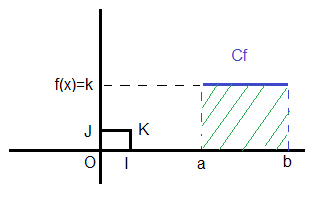
| ABCD مساحة | b ∫ a | f(x)dx=k(b-a)=S |
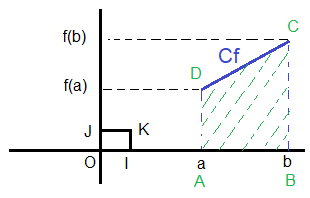
اذا كانت f(x)=mx+p
| b ∫ a | f(x)dx=[(m/2)x² + px] | b a |
هي مساحة شبه المنحرف ABCD
5.1.2 خاصية 1
اذا كانت f دالة متصلة على المجال I=[a;b]
فان مساحة حيز المحصور بين المنحنى Cf ومحور الافاصيل والمستقيمين (D): x=a و (D'): x=b هي:
| b ∫ a | |f(x)| dx .UA |
5.1.3 خاصية 2
لتكن f و g دالتين معرفتين ومتصلتين على I=[a;b]
مساحة جزء المستوى المحصور بين المنحنيين Cf و Cg والمستقيمين (D): x=a و (D'): x=b هي :
| b ∫ a | |f(x)-g(x)|dx.UA |
مثال
||i→||=2cm ; ||j→||=3cm
f(x)=(0,25)x² ; g(x)=x-1 و I=[0,5 ; 4]
| 4 ∫ 1/2 | |f(x)-g(x)| dx .UA = | 4 ∫ 0,5 | |(0,25)x²-1/x| dx .2.3 cm² = 6.8,10366 =48,62196 cm² |
5.2 حساب الحجوم
5.2.1 حجم مجسم
لتكن S(t) مساحة تقاطع مستوى مع مجسم , حجم المجسم المحدد بين المستويين , le Pa: x=a و Pb: x=b هو :
| b ∫ a | S(t)dx .UV |
5.2.2 حجم مجسم مولد بدوران
لتكن f دالة عددية متصلة على المجال I=[a;b], دوران المنحنى Cf دورة كاملة حول محور الافاصيل يولد مجسما , وتقاطع المستوى الذي معادلته x=t مع هذا المجسم هو دائرة مركزها f(t) ومساحتها π(f(t))²
| V= | b ∫ a | π (f(x))²dx .UV |