4.4 الدوال المثلثية

خاصية

1. الدالتان sin و cos متصلتين على IR.
2. الدالة tan متصلة على كل مجال على الشكل

]-	π	+kπ;	π	+kπ[ ; k∈ℤ
	2		2

تمرين

لتكن f دالة عددية معرفة كما يلي:

{	f(x)=	2x+sinx
		x
	f(0)=3

1. بين ان f دالة متصلة على IR*
2. هل الدالة f متصلة في 0?

تصحيح

1. لدينا f معرفة اذا كان x≠0 اذن D=IR*
الدالة x→2x+sinx هي مجموع دالتين متصلتين على IR وبالخصوص على IR*
الدالة x→x متصلة على IR وبالخصوص على IR*

بالاضافة انها لا تنعدم في IR*
اذن الدالة f متصلة على IR*
2. ندرس الاتصال في 0 لاحظ ان 0 ينتمي الى مجموعة التعريف لان f(0)=3

lim0f(x)=lim0	2x	+	sinx
	x		x

اذن lim₀f(x)=2+1=3=f(3)
اذن f متصلة في 0

5 الدالة √x

5.1 خاصية

الدالة x→√(x) متصلة على IR+

5.2 مثال

ادرس اتصال الدالة f:→sinx+√(x) على D.

تصحيح

1- f هي مجموعة دالتين , D=IR∩[0;+∞[ اذن D=[0;+∞[
2- لدينا sin متصلة على IR, اذن متصلة على [0;+∞[
et √ متصلة على [0;+∞[, اذن f متصلة على [0;+∞[.

6- الجزء الصحيح E(x)

6.1 تذكير

ليكن x عددا حقيقيا
E(x)=a ⇔ a≤ x < a+1 حيث a∈ℤ

6.2 امثلة

. E(0,5) = 0 ; E(3,14)=3
. E(-12,7)=-13 ; E(-√7)=-3
. E(4) = 4 ; E(-8)= -8

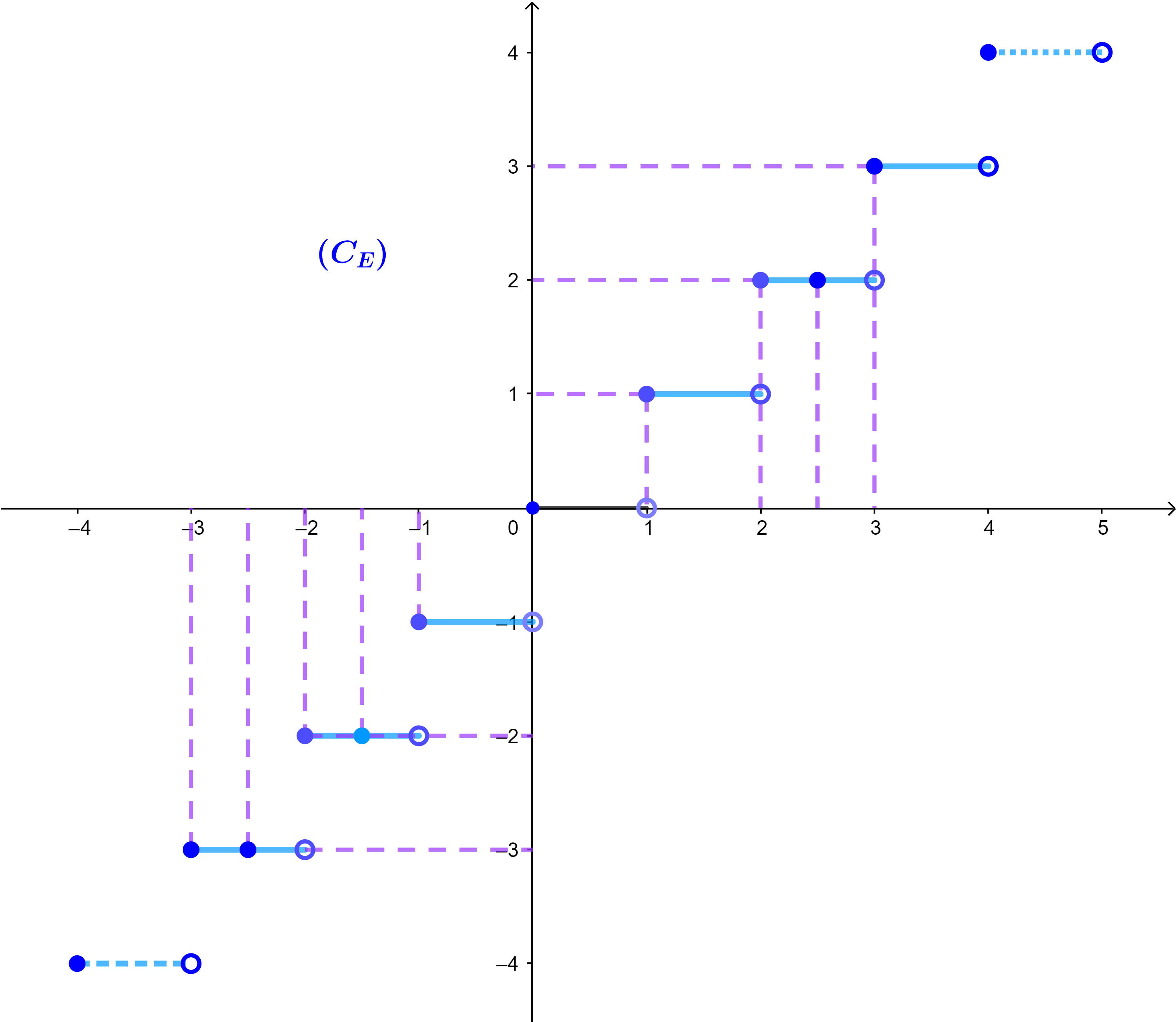
6.3 خاصية

الدالة E(x) غير متصلة على IR, ولكن متصلة في كل مجال من نوع [n;n+1[ حيث n∈ℤ .

7- صورة مجال بدالة متصلة

7.1 خاصية

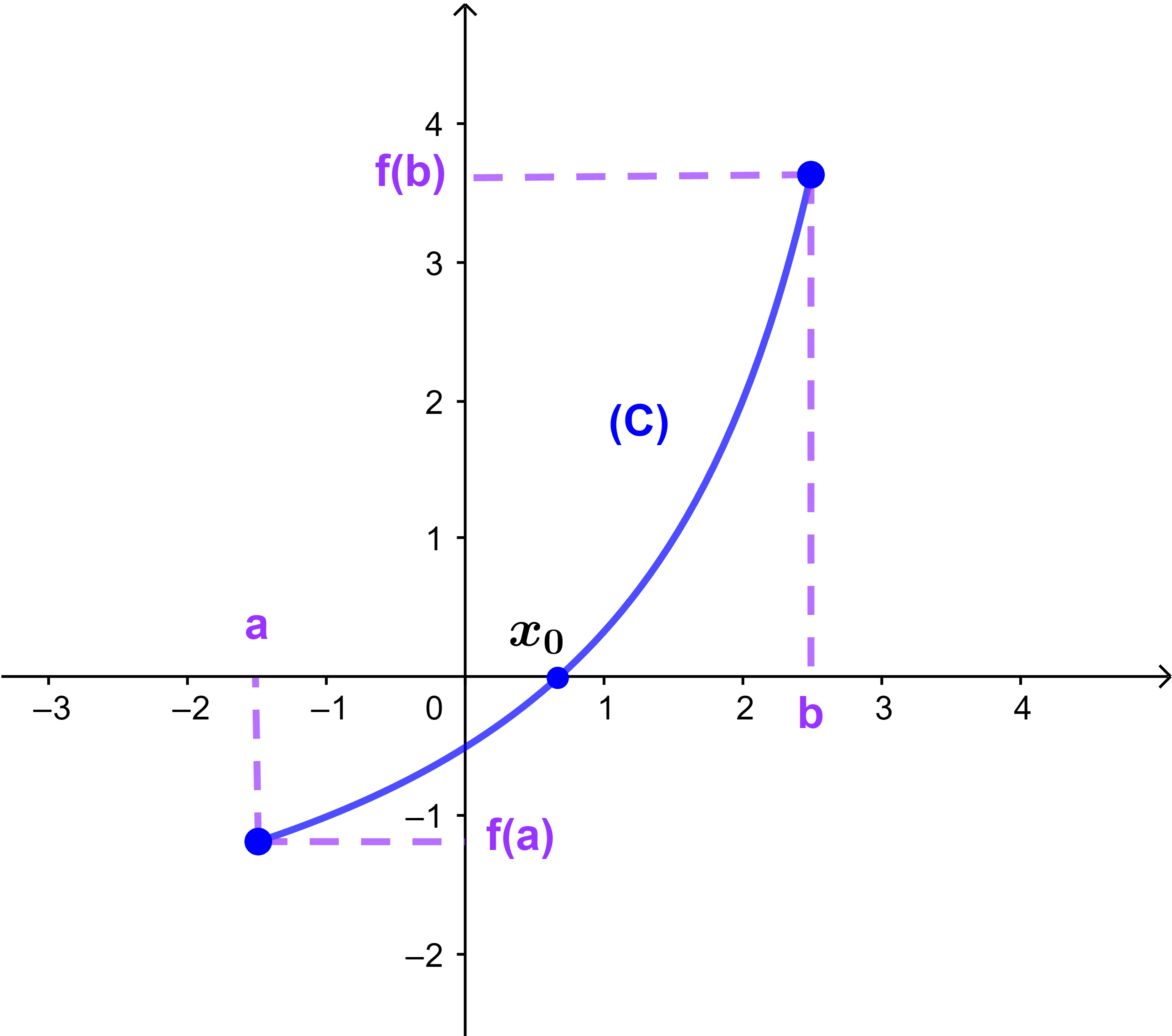
صورة قطعة طرفاها a و b بدالة متصلة هي قطعة
وصورة مجال بدالة متصلة هي مجال. ( ليس بالضرورة من نفس النوع )

مثال

f(x)=-1/x , 0< x< 1
f(x)=-x , 1≤x < 2
صورة المجال I=]0;2[ ب f هي f(I)=]-∞;-1].

7.2 خاصيات

متصلة f وتزايدية قطعا	متصلة f وتناقصية قطعا
f([a;b])=f[f(a);f(b)]	f([a;b])=[f(b;f(a))]
f(]a;b])=]lim>af(a);f(b)]	f(]a;b])=[f(b);lim>af(x)[
f([a; +∞[)=[f(a); lim+∞f(x)[)	f([a; +∞[)=]lim+∞f(x); f(a)])

تمرين 1

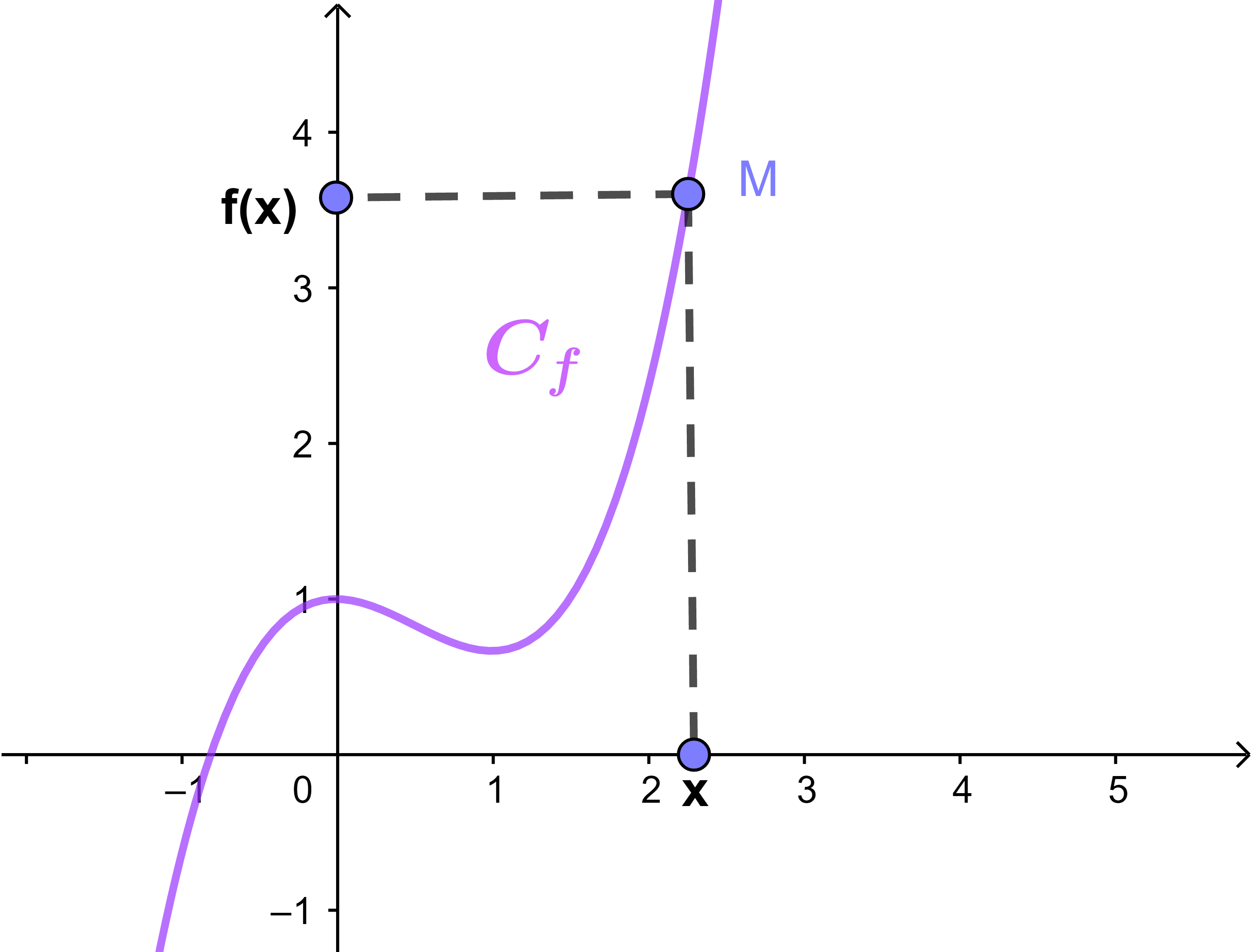
انطلاقا من منحنى الدالة f حدد صورة كل من المجالات التالية بواسطة الدالة f
[-2;-1] ; [-2;0] ; [0;2] ; [0;3]

تمرين 2

لتكن f دالة عددية معرفة كما يلي f(x)=x²+4x
حدد : f(]-∞;-3]) ; f([-2;0]) ; f([-1;+∞[)

8- اتصال مركب دالتين

8.1 خاصيات

8.1.1 خاصية 1

اذا f متصلة على I و g متصلة على J يتضمن f(I) فان الدالة gof متصلة على I.

8.1.2 خاصية 2 ; a→f(a)→g(f(a)

اذا f متصلة في a و g متصلة في f(a) فان gof متصلة في a

8.1.3 مثال

لتكن f دالة عددية معرفة كما يلي : f(x)=cos(2x+1)
ادرس اتصال الدالة f على Df

تصحيح

f مركبة cos والدالة التآلفية u:x→2x+1 لدينا u متصلة على IR و cos متصلة على IR اذن متصلة على u(IR)
ومنه فان f متصلة على IR.

8.1.4 نتيجة

اذا كانت f موجبة ومتصلة على I فان √f متصلة على I

تمرين

لتكن g دالة معرفة كما يلي :
g(x)= √(x²-1)-x ; ادرس اتصال g على Dg

8.2 خاصية (نهاية مركب دالة متصلة و دالة تقبل نهاية )

لتكن f دالة معرفة على مجال I و g دالة معرفة على مجال J يتضمن f(I) ; اذا lim_af(x)= L و g متصلة في L
فان lim_agof(x)=g(L)

تمرين

لتكن f دالة عددية معرفة كما يلي :

lim4f(x) احسب	f(x)=√(	x²-16	)
		x-4

9- مبرهنة القيم الوسيطة

9.1 مبرهنة

لتكن f معرفة ومتصلة على I=[a;b], a < b و m=minf(x) و M=maxf(x) لدينا
∀k∈[m;M])(∃x∈I): f(x)=k
وبتعبير آخر :
لكل عدد حقيقي k محصور بين f(a) و f(b), المعادلة f(x)=k تقبل حلا على الاقل في المجال[a;b] .

9.2 لازمة لمبرهنة القيمة الوسيطة

لتكن f دالة عددية متصلة ورتيبة قطعا على المجال [a;b], a< b
لكل عدد حقيقي k, محصور بين f(a) و f(b) المعادلة f(x)=k تقبل حلا وحيدا في المجال [a;b]

9.2.1 ملاحظة :

اذا f غير معرفة في a او في b , المبرهنة تبقى صحيحة باعتبار النهاية في a او في b.

9.2.2 نتيجة 1

اذا f متصلة على I=[a;b] و f(a).f(b) < 0 فان المعادلة f(x)= 0 تقبل حلا على الاقل في المجال I.

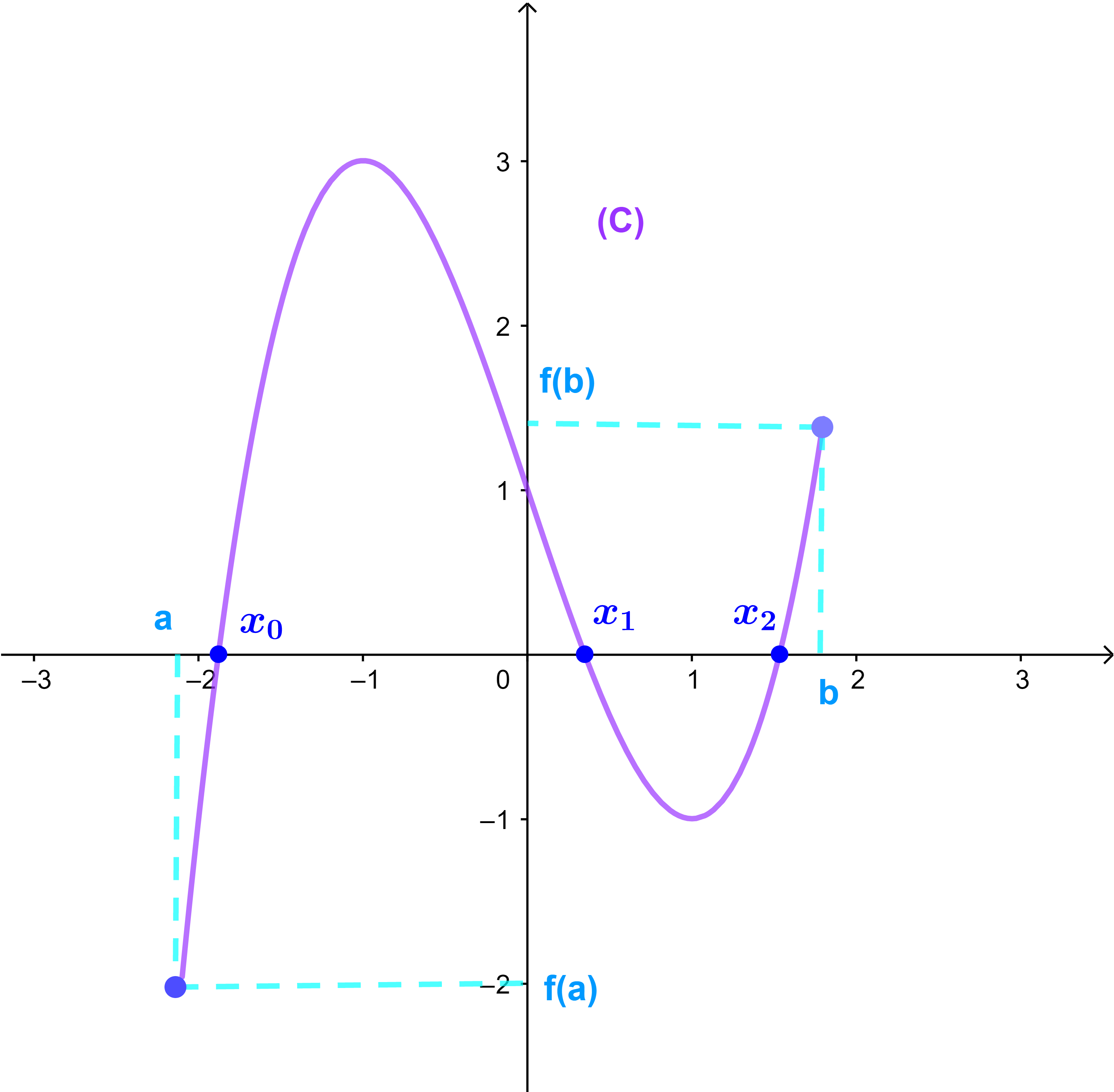
9.2.3 نتيجة 2

واذا f متصلة ورتيبة قطعا على المجال I و f(a).f(b) < 0 فان المعادلة f(x)= 0 تقبل حلا وحيدا x₀ في I
بحيث a< x₀< b.