دالة اللوغاريتم (1)
1- دالة اللوغاريتم النبيري
1.1 تعريف وخاصيات
1.1.1 تعريف
دالة اللوغاريتم النبيري ونرمز لها ب ln هي الدالة الاصلية الوحيدة للدالة العددية المعرفة على ]0;+∞[ بما يلي
| x→ | 1 |
| x |
التي تنعدم في العدد 1,اي ln(1)=0
1.1.2 نتائج
1) Dln=]0;+∞[
2) ln قابلة للاشتقاق على ]0;+∞[ ولدينا
| ∀x∈]0;+∞[: ln'(x)= | 1 |
| x |
اذن ln تزايدية قطعا على ]0;+∞[
1.1.3 خاصيات
اذا كان 0 < x < 1 فان lnx < 0
اذا كان x > 1 فان lnx > 0
∀x;y∈]0;+∞[, lnx=lny⇔x=y
∀x;y∈]0;+∞[, lnx< lny⇔x< y
تمرين 1
حل في IR المعادلة التالية
ln(x+1)=ln2x
تصحيح
المعادلة l(x+1)=ln2x معرفة ادا كان x+1>0 و
2x>0
اي اذا كان x>-1 et x>0 ومنه فان De=]0;+∞[
ليكن x∈]0;+∞[, l(x+1)=ln2x⇔x+1=2x
⇔ x+1=2x⇔x-2x+1=0⇔-x=-1
اذن x=1 وبما ان
1∈De اذن
1 هو حل للمعادلة
اذن S={1}
تمرين 2
حل في IR المعادلة التالية
ln(2x+2)=ln(x+5)
تصحيح
المعادلة ln(2x+2)=ln(x+5) معرفة اذا كان
2x+2>0 و x+5>0
اي x≥-1 و x≥-5
اذن المعادلة معرفة اذا كان x≥-1;( ناخذ الاكبر )
اذن De=]-1;+∞[
ليكن x∈]-1;+∞[,
ln(2x+2)=ln(x+5)⇔2x+2=x+5
⇔2x+2=x+4⇔2x+2-x=5
⇔x=5-2=3
وبما ان
3∈]-1;+∞[,
فان S={3}
1.1.4 الخاصيات الجبرية
ليكن x و y∈]0;+∞[
ln(xy)=lnx + lny
تمارين
1. اذا اخذنا ln2=0,7 و ln7=1,95
احسب ln(14)
2. اذا اخذنا ln25=3,2
احسب ln5
نتائج
ليكن x و y عددين موجبين قطعا
1) lnx² = 2lnx
2) ∀n∈IN, lnxn=nlnx
| ln( | 1 | )=-ln(y) (3 |
| y | ||
| ln( | x | )=ln(x)-ln(y) (4 |
| y |
| ln√(x)= | 1 | ln(x) (5 |
| 2 |
برهان ل 3 و 4:
| اذن | x>0, 1=x. | 1 |
| x |
| ln1= ln(x. | 1 | )=lnx+ln | 1 |
| x | x |
| ln1=0 لان | ln | 1 | =-lnx |
| x |
خاصية 4 هي نتيجة ل 3
| ln | x | = lnx+ln | 1 |
| y | y | ||
| ⇒ ln | x | = lnx-lny | |
| y |
1.1.5 خاصية
ليكن x>0 و r∈Q لدينا lnxr=rlnx
تمرين 1
بسط : ln8 + ln12 - ln18
تمرين 2
حل في IR:
1) lnx = 0 ;
2) lnx = 1
3) lnx = 3 ;
4) lnx = -2
تصحيح
1) المعادلة lnx=0, معرفة اذا كان x∈]0;+∞[
لدينا ln1=0 اذن
lnx=0⇔lnx=ln1
⇔x=1, 1∈]0;+∞[
اذن S={1}
2) lnx=1⇔lnx=lne ,(lne=1)
⇔x=e
اذن S={e}
3) lnx=3=3.1⇔lnx=3lne
⇔lnx=lne³
⇔x=e³
اذن S={e³}
lnx=-2⇔lnx=-2.1
⇔lnx=-2lne⇔lnx=lne-2
⇔x=e-2
اذن S={e-2}
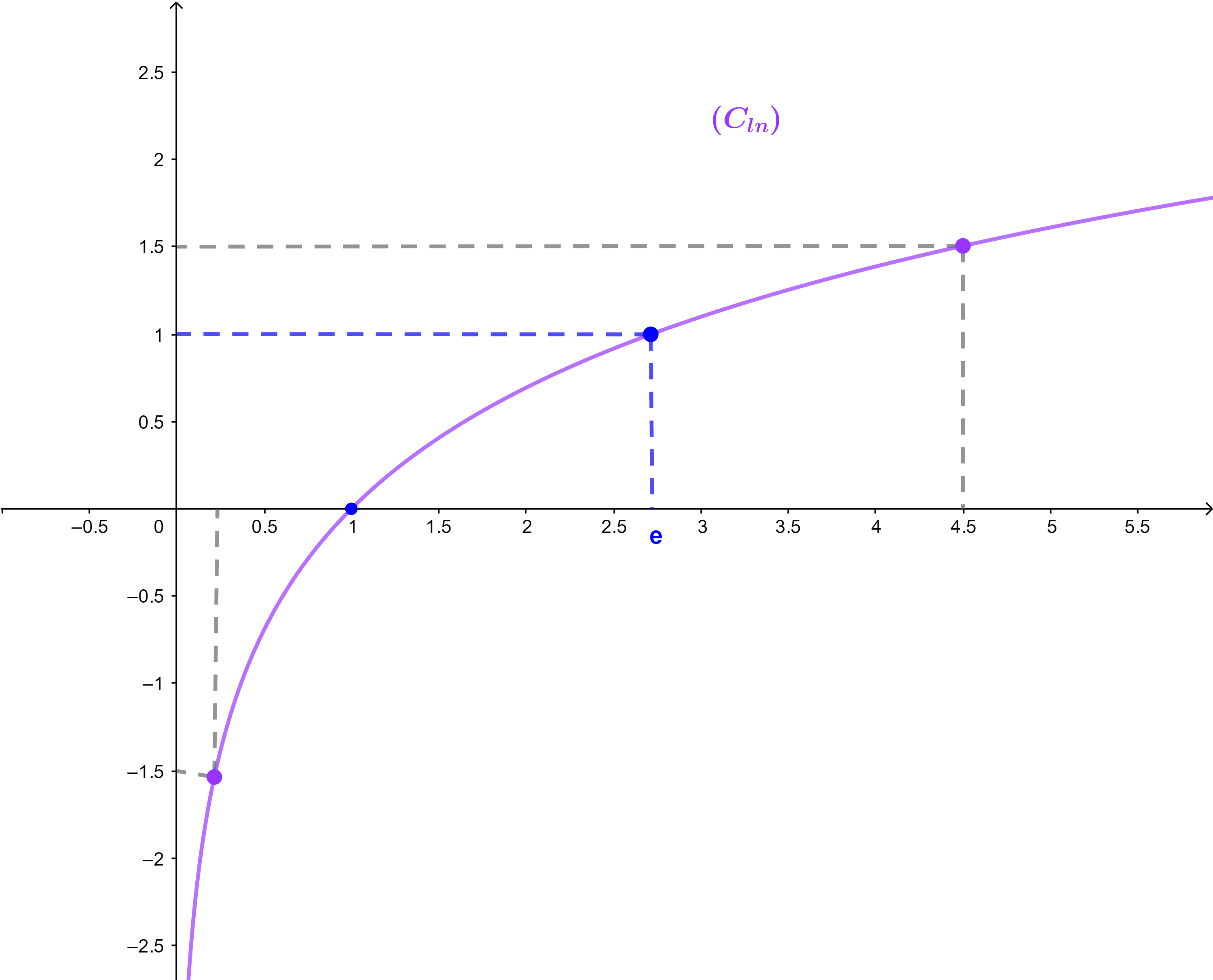
1.2 التمثيل المبياني للدالة x→lnx
1.2.1 مجموعة التعريف :
D=]0;+∞[
∃!e∈D: lne=1 ; e≃2,718
لان
1∈IR و الدالة ln متصلة وتزايدية قطعا على D
1.2.2 النهايات
lim+∞ lnx = +∞
و lim 0+ lnx = - ∞, اذن المنحنى (C) يقبل مقاربا معادلته x=0, (محور الافاصيل )
1.2.3 الوضع النسبي للمنحنى (C) والمستقيم (D):y=x
لدينا ∀x> 0; lnx< x
برهان
نعتبر الدالة g:x→x-lnx
نحسب g'(x) وندرس اشارتها
| x | 0 | 1 | +∞ | ||
| g'(x) | || | - | 0 | + |
g تناقصية قطعا على المجال
]0;1[
وتزايدية قطعا على المجال
]1;+∞[
اذن g تقبل قيمة دنوية في
1;
وبما ان g(1)=1>0 فان لكل x>0 لدينا lnx< x ومنه فان المنحنى (C) يوجد تحت المستقيم (D).
1.2.4 الفرع اللانهائي
المنحنى (C) يقبل فرعا شلجميا اتجاهه محور الافاصيل (Ox)
لان √x>0 اذن ln√x< √x اي
| 1 | lnx < √x |
| 2 |
عندما x→+∞ و x> e² يكون lnx>2 اي
| lnx | > | 2 |
| x | x |
| 1 | < | lnx | < | 1 |
| x | 2x | √x |
اذن
| lim∞ | ln(x) | =0 |
| x |
وبالتالي المنحنى C يقبل فرعا شلجميا في اتجاه (Ox)
1.1.4 الرتابة
| ∀x∈]0;+∞[; (ln)'(x)= | 1 | >0 |
| x |
ln'(x)> 0 يعني ان ln تزايدية قطعا على ]0;+∞[
1.1.5 المنحنى