1- الجداء السلمي في الفضاء

1.1 تعريف وخاصيات

1.1.1 انشطة

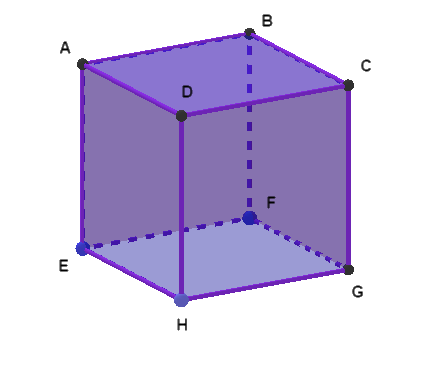
ABCDEFGH مكعب طول ضلعه 1
1. نتموضع في المستوى ABC
احسب AB^→.AC^→ و AB^→.AD^→
2. المستوى ABE احسب AB^→.AF^→

1.1.2 تعريف

الجداء السلمي لمتجهتين u^→ و v^→ ونكتب u^→.v^→ يساوي الجذاء السلمي للمتجهتين AB^→ و AC^→ في المستوى P=ABC حيث u^→=AB^→ و v^→=AC^→
u^→.v^→ = AB^→.AC^→ = AB^→.AH^→ حيث H المسقط العمودي للنقطة C على (AB).

1.1.3 منظم متجهة

تعريف 1

u^→ متجهة من V3
u^→.u^→ يسمى المربع السلمي للمتجهة u^→ ونرمز له ب u²^→
العدد الحقيقي الموجب √u²^→ المعين ل ||u^→|| هو منظم المتجهة u^→
اذا كانت u^→=AB^→ فان ||u^→||=AB

تعريف 2

u^→.v^→=||u^→|||v^→||cos(u^→;v^→)

1.2 خاصيات التماثلية وثنائية الخطية

1.2.1تعريف وخاصية

u^→ و v^→ و w^→ متجهات من V3 و t عددحقيقي غير منعدم
التماثلية او التبادلية u^→.v^→ = v^→.u^→/
ثنائية الخطية :
u^→.(v^→+w^→) = u^→.v^→ + u^→.w^→
u^→.(tv^→) = t(u^→.v^→) و

1.2.2 نتائج

(u^→+v^→)²=u²^→+v²^→+2u^→.v^→
(u^→-v^→)²=u²^→+v²^→-2u^→.v^→
(u^→-v^→).(u^→+v^→)=u²^→-v²^→
4u^→.v^→= (||u^→+v^→||²+||u^→-v^→||²)

تمرين

u^→ و v^→ متجهتان من V3 حيث ||u^→||=2 و ||v^→||=4 و u^→.v^→=-0,5
1. احسب u^→.(3u^→-v^→)
2. احسب ||u^→+v^→||

1.2.3 تعامد متجهتين

تعريف

نقول ان متجهتين متعامدتان اذا كان اتجاهما يحدد زاوية قائمة

خاصية

لتكن u^→ و v^→ متجهتين من V3.
u^→⊥v^→ ⇔ u^→.v^→=0
u → ↑v

برهان :

لدينا :
u^→.v^→ =||u^→||×||v^→||cos(u^→;v^→)
u^→.v^→=0
⇔ ||u^→||×||v^→||cos(u^→;v^→)=0
⇔ cos(u^→;v^→)=0 او ||u^→||=0 او ||v^→||=0
⇔
(u^→;v^→)≡π/2[π] او u^→=0^→ او v^→=0^→
⇔ u^→⊥v^→
للتذكير 0^→ متعامد مع كل متجهة.

1.3 اساس ممنظم في الفضاء

1.3.1 تعريف 1:

ثلاث متجهات غير مستوائية تحدد اساسا في V3

1.3.2 تعريف 2 :

(i^→;j^→;k^→) اساس في V3
(i^→;j^→;k^→) اساس متعامد ممنظم يعني i^→⊥j^→ و i^→⊥k^→ و j^→⊥k^→ و ||i^→||=||j^→||=||k^→||=1

1.3.3 خاصية:

(i^→;j^→;k^→) اساس في V3
⇔
(∀u^→∈V3)(∃a;b;c∈IR): u^→= ai^→+bj^→+ck^→

1.4 الصيغة التحليلية في V3

1.4.1 المعلم المتعامد الممنظم

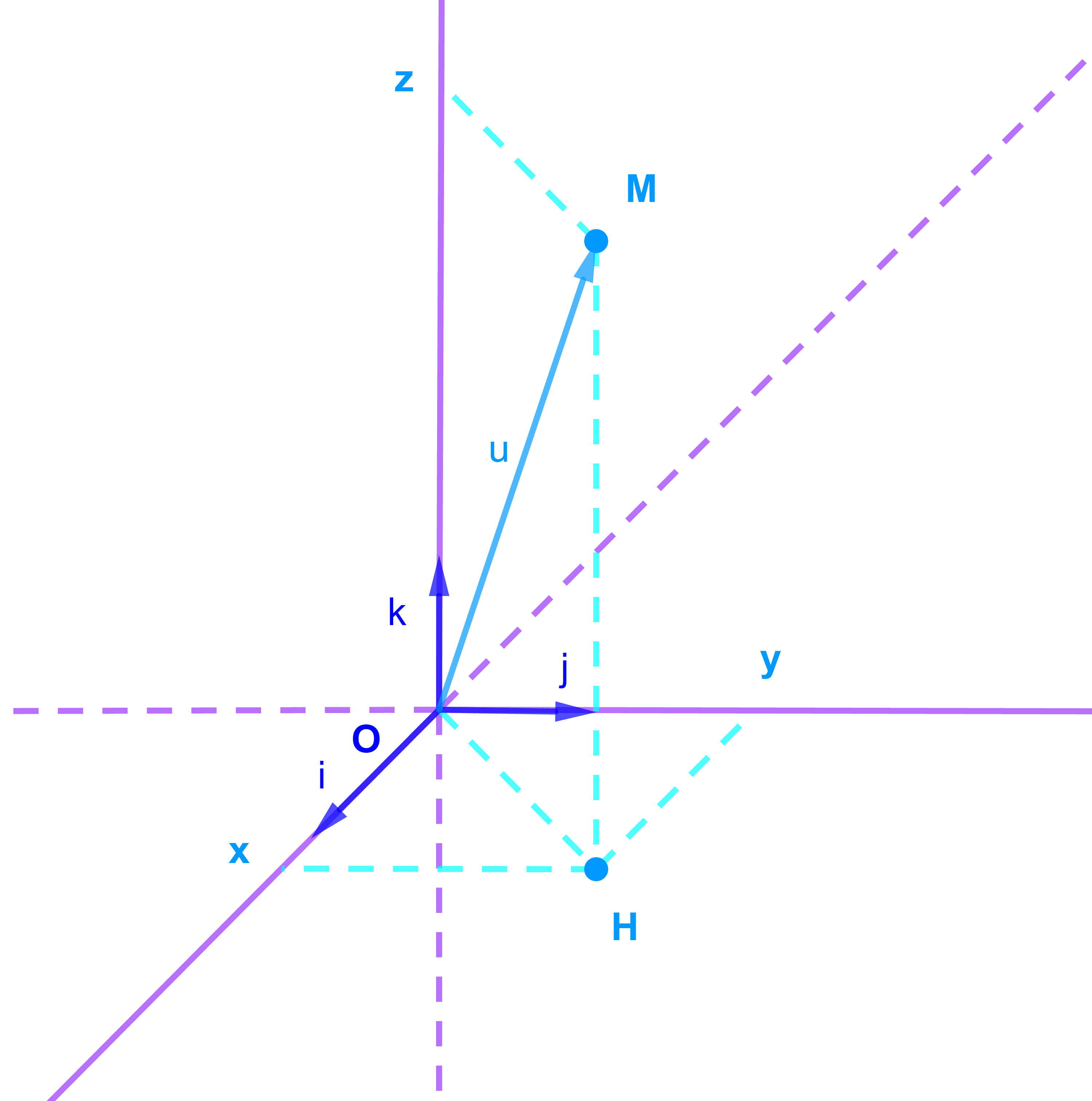
(i^→;j^→;k^→) اساس متعامد ممنظم في V3 و O نقطة من الفضاء E3 المربوع (O;i^→;j^→;k^→) هو معلم متعامد ممنظم.

خاصية

(∀M∈E)(∃(x;y;z)∈IR³):
OM^→=xi^→+yj^→+zk^→
في هذا الدرس الفضاء منسوب الى معلم متعامد ممنظم (O;i^→;j^→;k^→)

1.4.2 خاصية

u^→(x:y:z) و v^→(x';y';z') متجهتان من الفضاء
u^→.v^→= xx + yy +zz
تبيان : يكفي تطبيق التماثلية وثنائية الخطية للجداء السلمي

1.4.3 امثلة

u^→(1;2;3) ; v^→(-2;3-;-1)
u^→.v^→ = 1.(-2)+2.3+3.(-1)=1
u^→(-2;8;2) ; v^→(-1;-2;7)
u^→.v^→=(-2).(-1)+8.(-2)+2.7 = 0
اذن u^→ و v^→ متعامدتان

1.4.4 منظم متجهة

u^→ متجهة من V3, ||u^→||=√u² اذن
||u^→||=√(x²+y²+z²)

امثلة :

u^→(2;0;3), ||u^→||=√(4+0+9)=√13

1.4.5 المسافة AB

AB=||AB^→|| اذن
AB = √((x-x)²+(y-y)²+(z-z)²)

مثال:

A(1;-1;2) ; B(5;2;2)
AB=√((5-1)²+(2-(-1))²+(2-2))
=√25=5

تمرين

(ABC) مثلث حيث AB=2 و AC=4 و AB^→.AC^→=-2
1) بين ان BC²=AB²+AC²-2AB^→.AC^→
2) استنتج المسافة BC
3) احسب BA^→.BC^→
4) استنتج قياسا بالتقريب للزاوية (BA^→;BC^→) .