1- Produit scalaire dans l'espace

1.1 Définition et propriétés

1.1.1 Activité

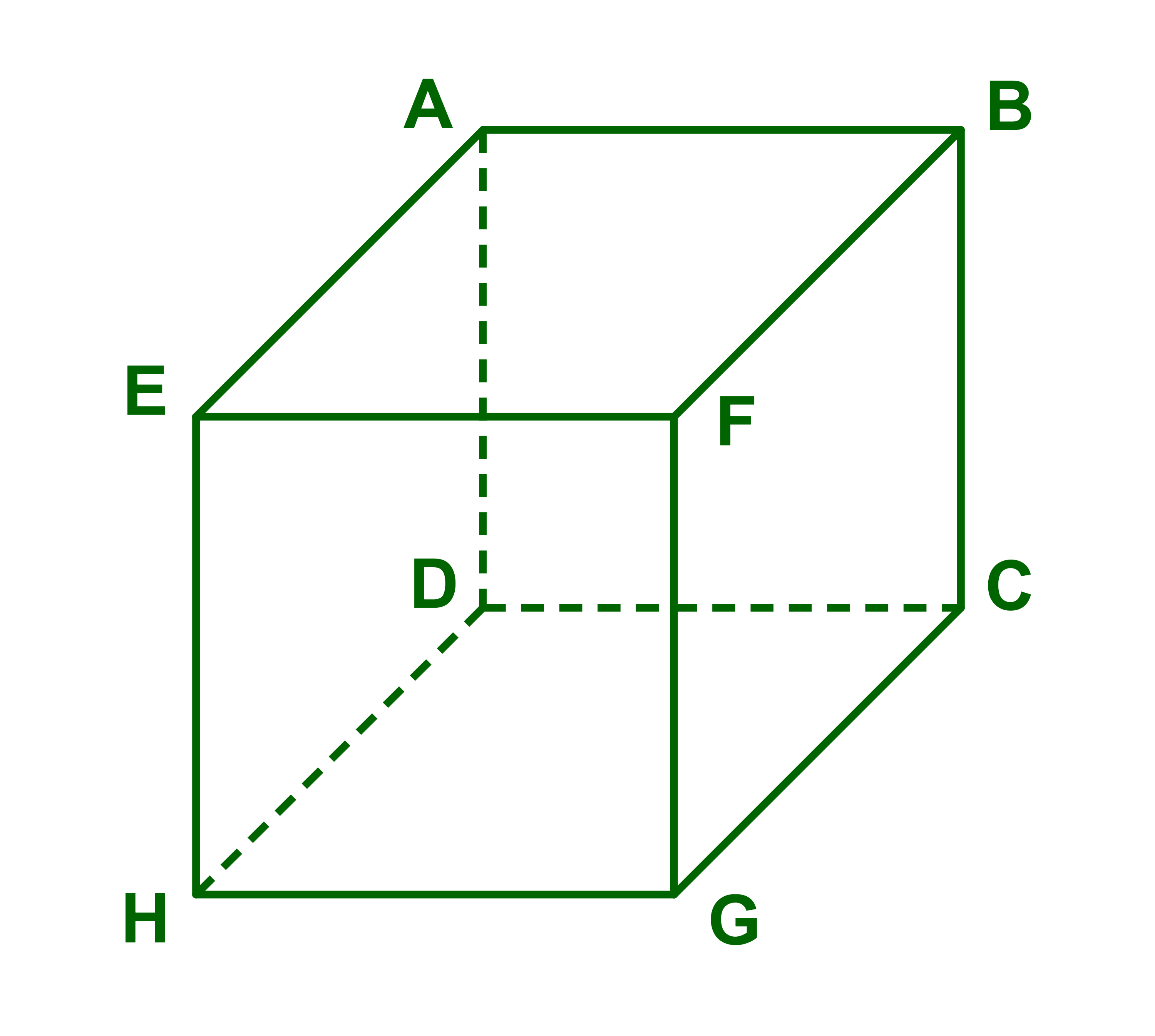
Soit ABCDEFGH un cube d'arret 1.
1) On se place dans le plan ABC
Calculer AB^→.AC^→ et AB^→.AD^→.
2) On se place dans le plan ABE
Calculer AB^→.AF^→.

1.1.2 Définition

Soient u^→ et v^→ deux vecteurs dans l'espace tels que u^→=AB^→ et v^→=AC^→.
Le produit scalaire de u^→ et v^→ est égal au produit scalaire des vecteurs AB^→ et AC^→ calculé dans le plan P=ABC et est noté u^→.v^→.
u^→.v^→=AB^→.AC^→=AB^→.AH^→ tel que H est le projeté orthogonal de C sur (AB).

1.1.3 Norme d'un vecteur

Définition Soit u^→ un vecteur.
Le nombre réel u^→.u^→ est appelé le carré scalaire du vecteur u^→ et est noté u²^→.
Le réel positif √u²^→ est la norme du vecteur u^→ et est noté ||u^→||.
Si u^→=AB^→ alors ||u^→||=AB.

Propriété Soient u^→ et v^→ deux vecteurs.
u^→.v^→=||u^→||×||v^→||×cos(u^→;v^→).

1.2 Symétrie et bilinéarité

1.2.1 Propriété et définition

Soient u^→ ; v^→ et w^→ trois vecteurs dans V₃ et t un nombre réel non nul.
1) Symétrie ou commutativité
u^→.v^→ = v^→.u^→.
2) Bilinéarité
u^→.(v^→+w^→) = u^→.v^→ + u^→.w^→.
Et u^→.(tv^→) = t(u^→.v^→).

Résultats
(u^→+v^→)²=u²^→+v²^→+2u^→.v^→.
(u^→-v^→)²=u²^→+v²^→-2u^→.v^→.
(u^→-v^→).(u^→+v^→)=u²^→-v²^→.
4u^→.v^→= (||u^→+v^→||²+||u^→-v^→||²).

Exercice 1 tp

Soient u^→ et v^→ deux vecteurs dans V₃
tels que ||u^→||=2, ||v^→||=4 et u^→.v^→ = -0,5.
1) Calculer u^→.(3u^→-v^→).
2) Calculer ||u^→+v^→||.

1.2.2 Orthogonalité de deux vecteurs

Définition
Deux vecteurs sont orthogonaux si leurs directions forment un angle droit.

Propriété
Soient u^→ et v^→) deux vecteurs dans V₃.
u^→⊥v^→ ⇔ u^→.v^→=0.
u → ↑v

Démonstration on a
u^→.v^→=||u^→||×||v^→||cos(u^→;v^→).

u^→.v^→=0 ⇔ ||u^→||×||v^→||cos(u^→;v^→)=0
⇔ cos(u^→;v^→)=0 ou ||u^→||=0 ou ||v^→||=0

ou u^→=0^→ ou v^→=0^→
⇔ u^→⊥v^→
Notons que le vecteur 0^→ est orthogonal à tout vecteur.