Exercice 1 tp

Soit (ABC) un triangle tel que AB=2 ; AC=4 et AB^→.AC^→=-2.
1) Montrer que BC²=AB²+AC²-2AB^→.AC^→.
2) Déduire BC.
3) Calculer BA^→.BC^→.
4) Déduire une mesure de l'angle (BA^→;BC^→) arrondie au degré près.

1.3 base orthonormée

1.3.1 Définition 1

Trois vecteurs non coplanaires déterminent une base dans V₃.

1.3.2 Définition2

Soit B=(i^→;j^→;k^→) une base dans V₃
(i^→;j^→;k^→) est une base orthonormée signifie i^→⊥j^→ ; i^→⊥k^→ ; j^→⊥k^→
et ||i^→||=||j^→||=||k^→||=1.

1.3.3 Propriété

B=(i^→;j^→;k^→) est une base dans V₃
⇔(∀u^→∈V₃) (∃a;b;c∈IR)
u^→= ai^→+bj^→+ck^→.
Le triplet (a;b;c) détermine les coordonnées du vecteur u^→ dans la base B et on écrit u^→(a;b;c).

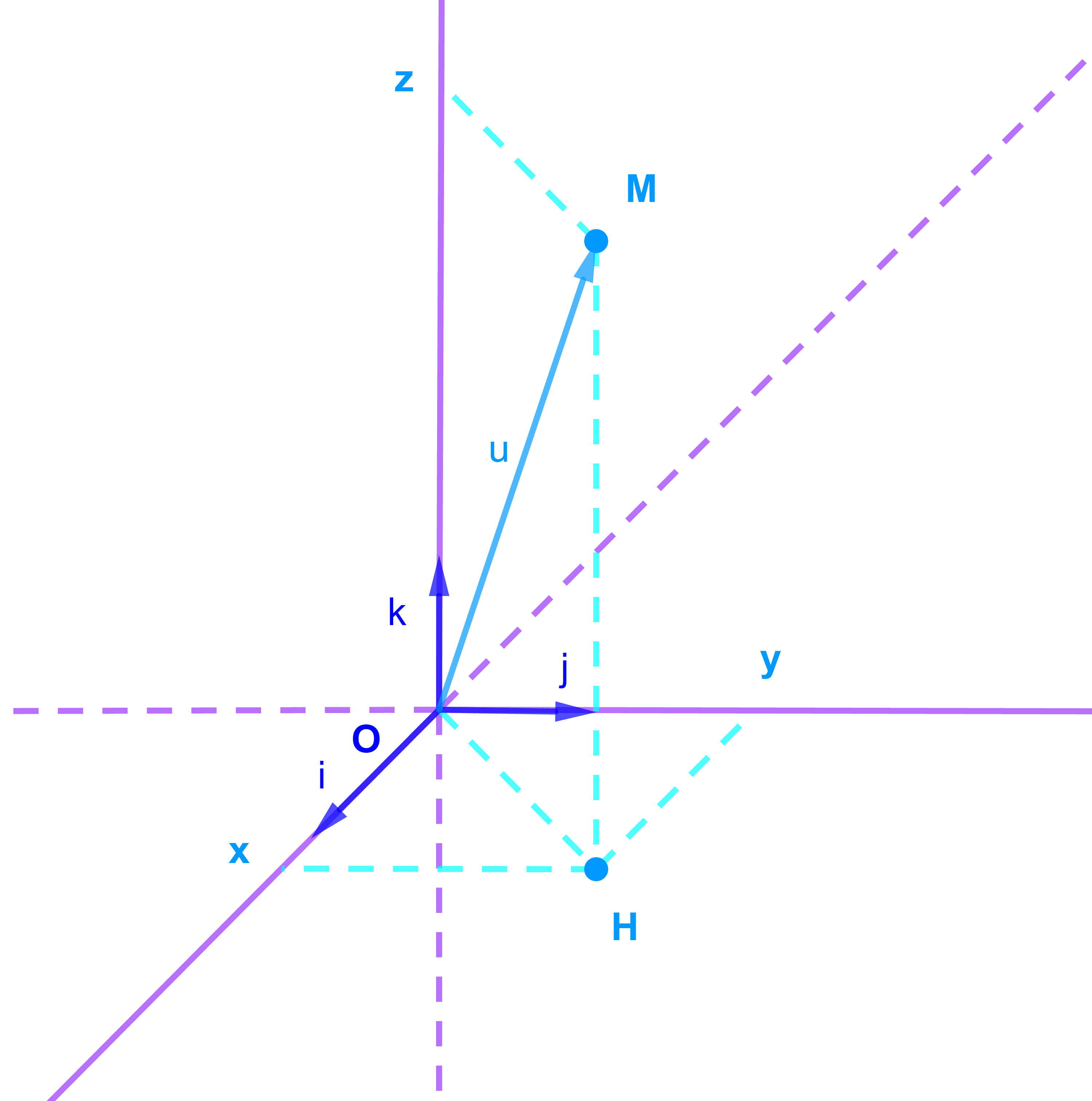
1.4 Expression analytique dans V₃

1.4.1 Repère orthonormé

Soient (i^→;j^→;k^→) une base orthonormée dans V₃ et O un point dans l'espace E₃.
Le quadruplet (O;i^→;j^→;k^→) est un un repère orthonormé dans l'espace E₃.

Propriété

(∀M∈E₃)(∃(x;y;z)∈IR³)
OM^→=xi^→+yj^→+zk^→.

Désormais l'espace est rapporté au repère orthonormé (O;i^→;j^→;k^→).

1.4.2 Propriété

Soient u^→(x:y:z) et v^→(x';y';z') deux vecteurs dans l'espace E₃.
u^→.v^→ = xx + yy +zz.

(Il suffit d'appliquer la symétrie et la bilinéarité du produit scalaire).

Exemples
1) Soient u^→(1;2;3) et v^→(-2;3-;-1) deux vecteurs.
u^→.v^→=1.(-2)+2.3+3.(-1)=1.

2) Soient u^→(-2;8;2) et v^→(-1;-2;7) deux vecteurs.
u^→.v^→=(-2).(-1)+8.(-2)+2.7 = 0.
Dans ce ca u^→ et v^→ sont donc orthogonaux.

1.4.3 Norme d’un vecteur

Soit u^→(x;y;z) un vecteur dans V₃.
||u^→||=√u²=√(x²+y²+z²).

Exemple
Soit u^→(2;0;3) un vecteur.
||u^→||=√(4+0+9)=√13.

1.4.4 Distance AB

Soient A et B deux points dans l'espace E₃.
La distance AB est définie par AB=||AB||
ou encore AB=√((x_B-x_A)²+(y_B-y_A)²+(z_B-z_A)²).

Exemple
Soient A(1;-1;2) et B(5;2;2) deux points dans l'espace E₃.
AB=√((5-1)²+(2-(-1))²+(2-2))=√25
donc AB=5.