Produit scalaire (3)
2- L'ensemble P={M(x;y;z)/u→.AM→=k}
2.1 Propriétés
2.1.1 Introduction
L'espace est rapporté à un repère orthonormé (O;i→;j→;k→).
Soient u→(a;b;c)∈V3
et A(xA;yA;zA)∈E3.
On considère l'ensemble
P ={M(x;y;z)∈E3/u→.AM→=k tel que k∈IR}
M(x;y;z)∈P ⇔ a(x-xA)+b(y-yA)+c(z-zA)=k
⇔ ax+by+cz+(-axA-byA-czA-k)=0.
On pose d=-axA-byA-czA-k.
M(x;y;z)∈P ⇔ ax+by+cz+d=0.
2.1.2 Propriétés
L'espace est rapporté à un repère orthonormé (O;i→;j→;k→).
1) Soient A∈E3 et u→(a;b;c)∈V3.
L'ensemble des points M de l'espace E3 tels que
u→.AM→=k et k∈IR est
un plan.
2) Tout plan admet une équation cartésienne sous la forme
ax+by+cz+d=0 tels que a;b et c sont des nombres réels non tous nuls.
Exemple
Soient A(1;2;3) un point dans E3 et u→(5;-1;4)
un vecteur dans V3.
Déterminer l'ensemble
ℙ={M(x;y)/ u→.AM→=5}.
Correction
5x-y+4z+d=0 est une équation du plan ℙ.
A∈ℙ donc le triplet (1;2;3) vérifie l'équation du plan
5-2+12+d=0 ou encore d=-15
ainsi ℙ: 5x-y+4z-15=0.
2.2 Plan défini par son vecteur normal
2.2.1 Définition
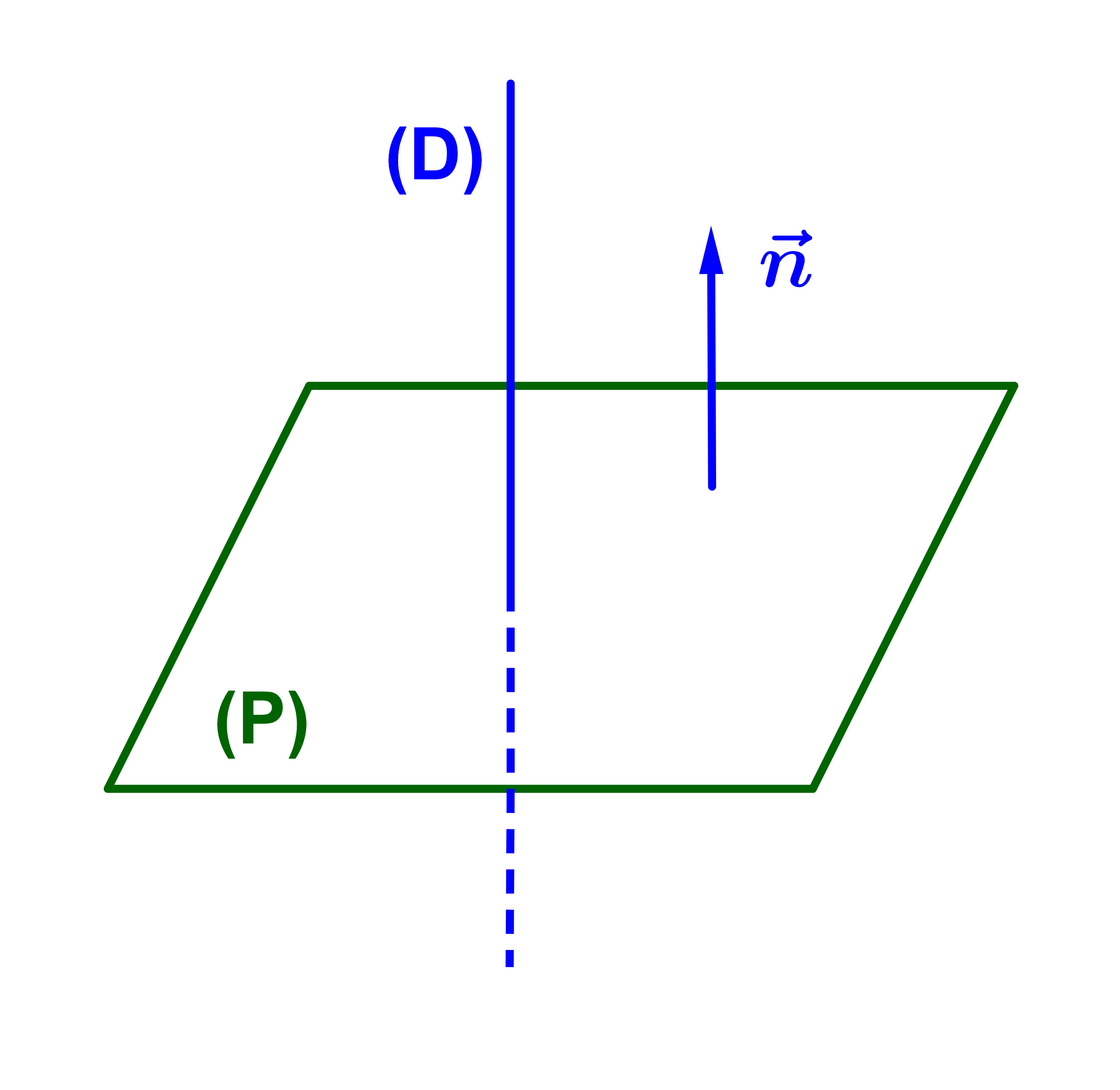
On dit qu'un vecteur n→ est normal au plan ℙ si n→ est un vecteur directeur d'une droite orthogonale à ℙ.
2.2.2 Equation cartésienne d’un plan
Théorème
L'espace est rapporté à un repère orthonormé (O;i→;j→;k→).
Soit ℙ un plan de vecteur normal n→(a;b;c)
et passe par un point A(xA;yA;zA).
M(x;y;z) ∈ ℙ ⇔ u→.AM→=0
⇔ ax+by+cz+d=0
tel que d=-(axA+byA+czA).
Résultat
Toute équation de la forme
ax+by+cz+d=0 définit un plan de vecteur normal n→(a;b;c) tels que a;b et c non tous nul.
Exemple
L'équation 2 x+3 y+7z+10 = 0 définit un plan ℙ de vecteur normal n→(2;3;7).
2.2.3 Distance d’un point à un plan
Soient B(x;y;z) un point et ℙ un plan d'équation ax+by+cz+d=0. On a d(B;ℙ)=BH tel que H est le projeté orthogolal de B sur le plan ℙ et n→ est un vecteur normal à P.
Donc n→ et BH→ sont colinéaires
et donc |BH→.n→|=BH||n→||.
Propriété
L'espace est rapporté à un repère orthonormé (O;i→;j→;k→).
La distance d'un point B(xB;yB;zB) à un plan
ℙ: ax+by+cz+d=0 est définie comme suit
| BH = | |BH→.n→| |
| ||n→|| | |
| d(B ; P) = | | axB+byB+czB+d | |
| √(a²+b²+c²) |
Exemple
Soient B(1;2;3) un piont dans l'espace E3
et ℙ: 2x+5y+z+1=0 un plan.
Calculer d(B;ℙ).
Correction
| d(B;ℙ) = | |2.1+5.2+1.3+1| |
| √(4+25+1) | |
| = | 8√30 |
| 15 |