Droite dans le plan (10)
Exercice 1 tp
Le plan ℙ est rapporté à un repère orthonormé
(O;i→;j→). On considère dans ℙ deux droites
(D): x-2y+3=0 et (D'): 2x+y+1=0.
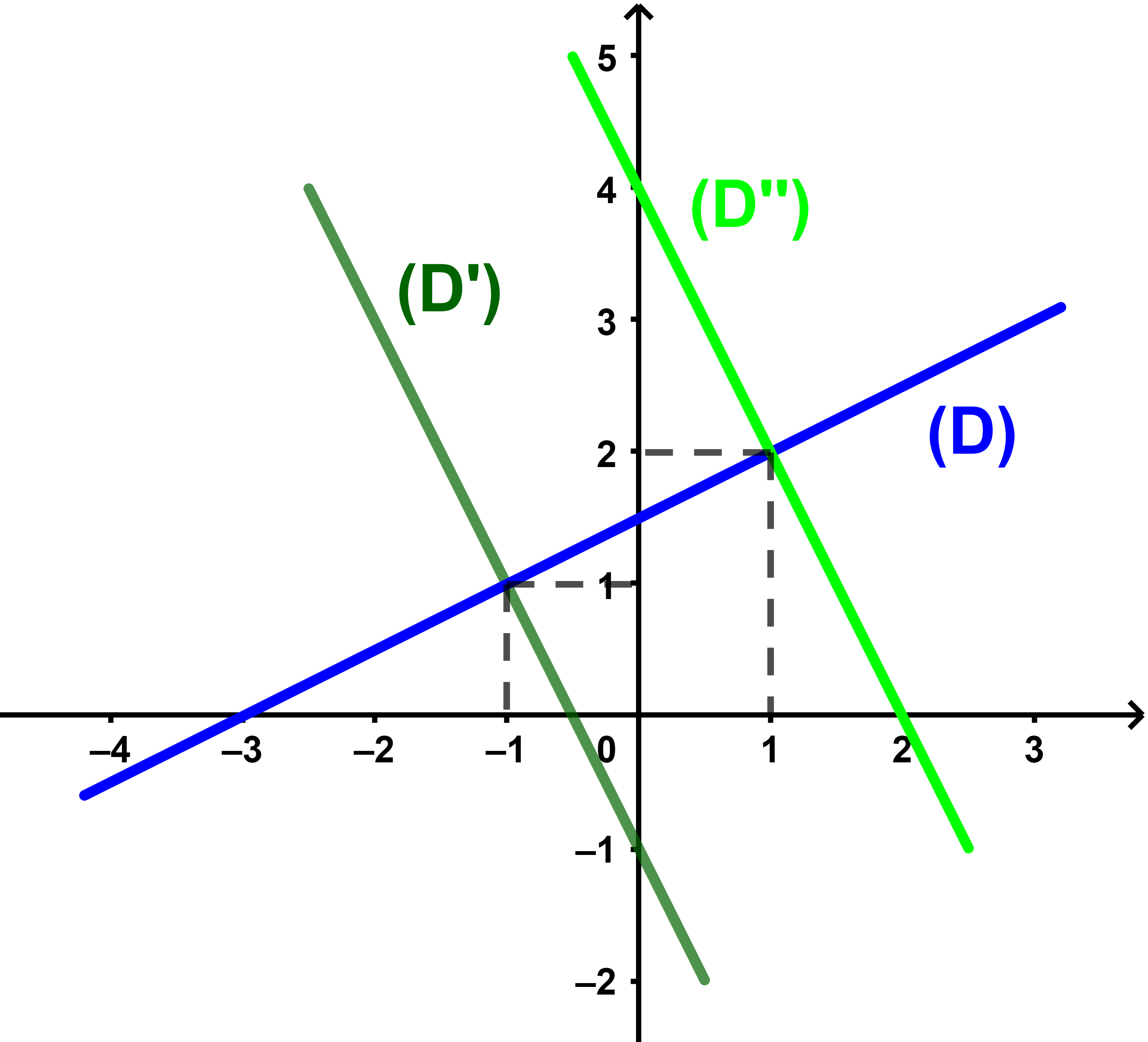
1) Construire (D) et (D).
2) Montrer que (D)⊥(D').
3) Déterminer l'intersection de (D) et (D').
4) Déterminer une équation d'une droite (D") passant par E(2;0) et perpendiculaire avec (D)
5) Etudier la position relative de (D') et (D").
Correction
1) Notons que pour tracer une droite on trace d'abord deux points de cette droite.
| x = -3 | et | y = 0 | → | A(-3 ; 0)∈(D) |
| x = 1 | et | y = 2 | → | B'(1 ; 2)∈(D) |
(D) passe par A et B donc (D)=(َAB).
| x = 0 | et | y = -1 | → | A'(0 ; -1)∈(D') |
| x = -1 | et | y = 1 | → | B(-1 ; 1)∈(D') |
(D') passe par A' et B'
donc (D')=(A'B')
2) On détermine le coefficient directeur de (D)
x-2y+3=0 signifie 2y=x+3 signifie
| y = | 1 | x + | 3 |
| 2 | 2 |
donc
| m = | 1 |
| 2 |
m=(0,5) est le coefficient directeur de (D).
On détermine le coefficient directeur de (D').
2x+y+1=0 signifie y=-2x-1.
m'=-2 est le coefficient directeur de (D')
Puisque m.m =-1 alors (D)⊥(D').
3) On résout le système ci-dessous pour déterminer le point d'intersection
| { | y = -2x - 1 |
| x - 2y + 3 = 0 |
Pour cela on peut utiliser la méthode de substitution.
| { | y = -2x - 1 |
| x - 2(-2x - 1) + 3 = 0 |
signifie
| { | y = -2x - 1 |
| 5x = -5 |
donc
| { | y = - 2. | (-1) | - 1 = 1 |
| x = | - 5 | = -1 | |
| 5 |
Ainsi
| { | y = | 1 |
| x = | -1 |
Alors (D) ∩ (D') = {E(-1;1)}.
4) (D)⊥(D") donc m.m"=-1 et donc m"=-2
ainsi l'équation de (D") s'écrit sous la forme
y=-2x+p".
Et puisque E∈(D") alors le couple (2;0) vérifie l'équation
donc 0=-2.2+p" ou encore p"=4
ainsi (D"): y=-2x+4.
Ou encore (D"): 2x+y-4=0.
5) (D)⊥(D') et (D)⊥(D") donc (D')||(D")
On doit savoir si (D') et (D") sont strictement parallèles ?
On a A'(0;-1)∈(D') est ce que A'(0;-1)∈(D") ?
(D") : y=-2x+4
-1=-2.0+4 signifie -1=4 ce n'est pas possible donc A'(0;-1)∉(D")
ainsi (D') ≠ (D") alors elles sont strictement parallèles.