Droite dans le plan (9)
Exercice 1 tp
Le plan ℙ est rapporté à un repère orthonormé
(O;i→;j→). On considère dans ℙ deux droites
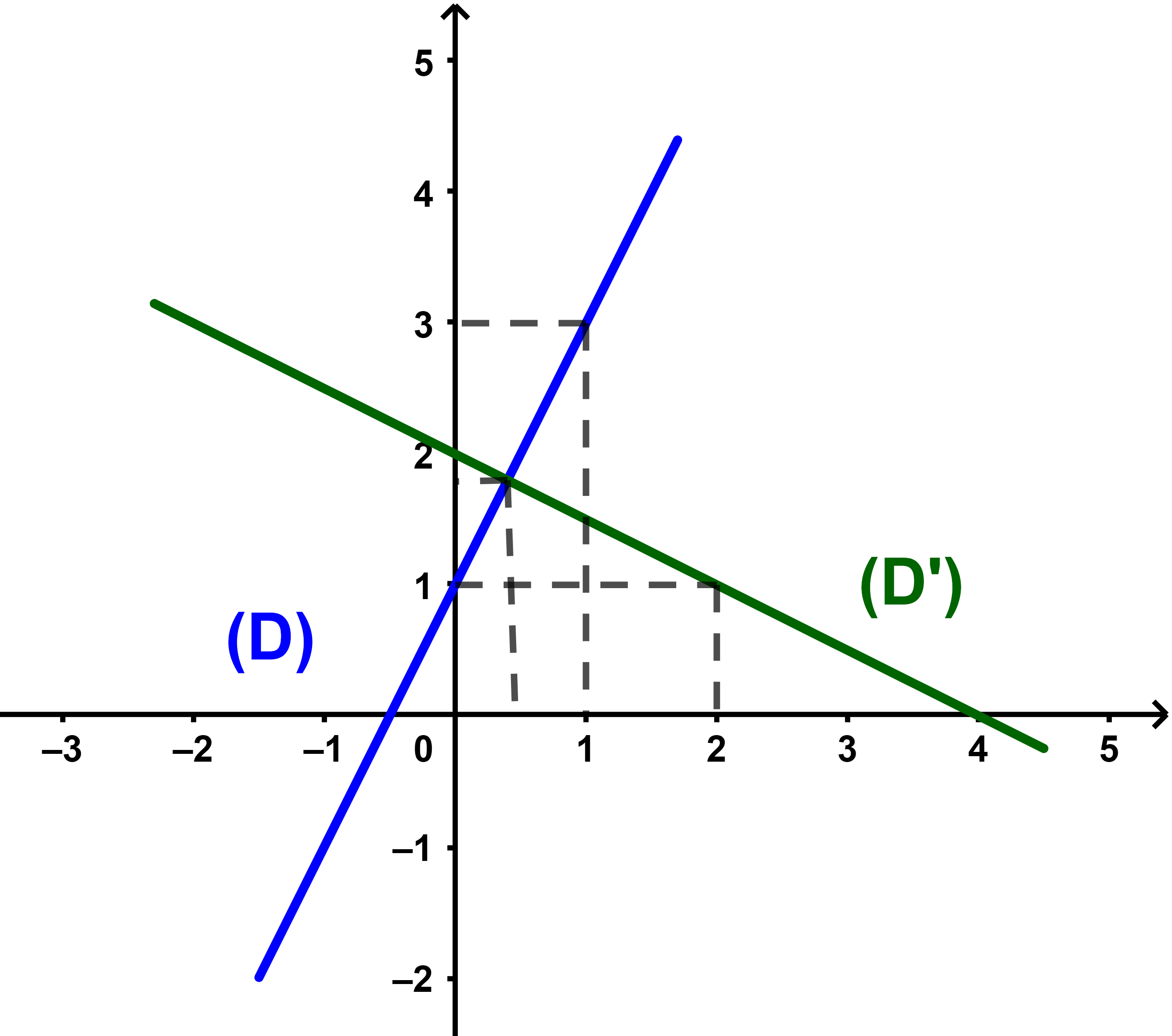
(D): y=2x+1 et (D'): x+2y-4=0.
1) Construire (D) et (D).
2) Montrer que (D)⊥(D').
3) Déterminer l'intersection de (D) et (D').
Correction
1) Notons que pour tracer une droite on trace d'abord deux points de cette droite.
| x = 0 | et | y = 1 | → | A(0 ; 1)∈(D) |
| x = 1 | et | y = 3 | → | B'(1 ; 3)∈(D) |
(D) passe par A et B donc (D)=(َAB).
| x = 0 | et | y = 2 | → | A'(0 ; 2)∈(D') |
| x = 2 | et | y = 1 | → | B(2 ; 1)∈(D') |
(D') passe par A' et B'
donc (D')=(A'B').
2) m=2 le coefficient directeur de (D).
On détermine le coefficient directeur
de (D'): x+2y-4=0.
| y = | -1 | x + 2 |
| 2 |
donc
| m' = | -1 |
| 2 |
m'=-(0,5) est le coefficient directeur de (D').
Puisque m.m' = -1 alors (D)⊥(D').
3) Pour déterminer le point d'intersectionn on résout le système suivant .
| { | y = 2x + 1 |
| x + 2y - 4 = 0 |
Pour cela on peut utitiser la méthode de substitution
| { | y = 2x + 1 |
| x + 2(2x + 1) - 4 = 0 |
Signifie
| { | y = 2x + 1 |
| 5x = 2 |
donc
| { | y = 2. | 2 | + 1 |
| 5 | |||
| x = | 2 | ||
| 5 |
Ainsi
| { | y = | 9 |
| 5 | ||
| x = | 2 | |
| 5 |
alors
| (D) ∩ (D') = { E( | 2 | ; | 9 | ) } |
| 5 | 5 |
Exercice 2 tp
Le plan ℙ est rapporté à un repère orthonormé
(O;i→;j→). On considère dans ℙ deux droites
(D): y=-x+1 et (D'): y=x+1
1) Construire (D) et (D').
2) Montrer que (D)⊥(D').
3) Déterminer l'intersection de (D) et (D').