3.3 تجويه المستوى

3.3.1 اشارة ax+by+c

المستوى ℙ منسوب الى معلم متعامد ممنظم (O;i^→;j^→). نعتبر مستقيم
(D): ax+by+c=0
(D) يحدد نصفي مستوى حدودهما هو (D)
نصفي مستوى معرف بالمتراجحة
ax+by+c<0
ونصف المستوى الآخر محدد بالمتراجحة
ax+by+c>0.

ملاحظة
اذا كان زوج احداثيتا نقطة A لا تنتمى الى المستقيم (D) ويحقق احدى المتراجحتين فان هذه المتراجحة تحدد نصف المستوى الذي يحتوي على النقطة A
في الغالب نختار النقطة O اذا كانت O∉(D).

3.3.2 مثال 1

1) ادرس اشارة العدد x+y-2
ثم حل مبيانيا المتراجحة x+y-2<0.

2) ادرس اشارة العدد x-y+2
ثم حل مبيانيا المتراجحة x-y+2>0.

3) حل مبيانيا المتراجحة
(I): (x+y-2)(x-y+2)<0
استنتج حلول النظمة

{	x + y - 2 > 0
	x - y + 2 < 0

تصحيح
1) (a) اشارة x+y-2.
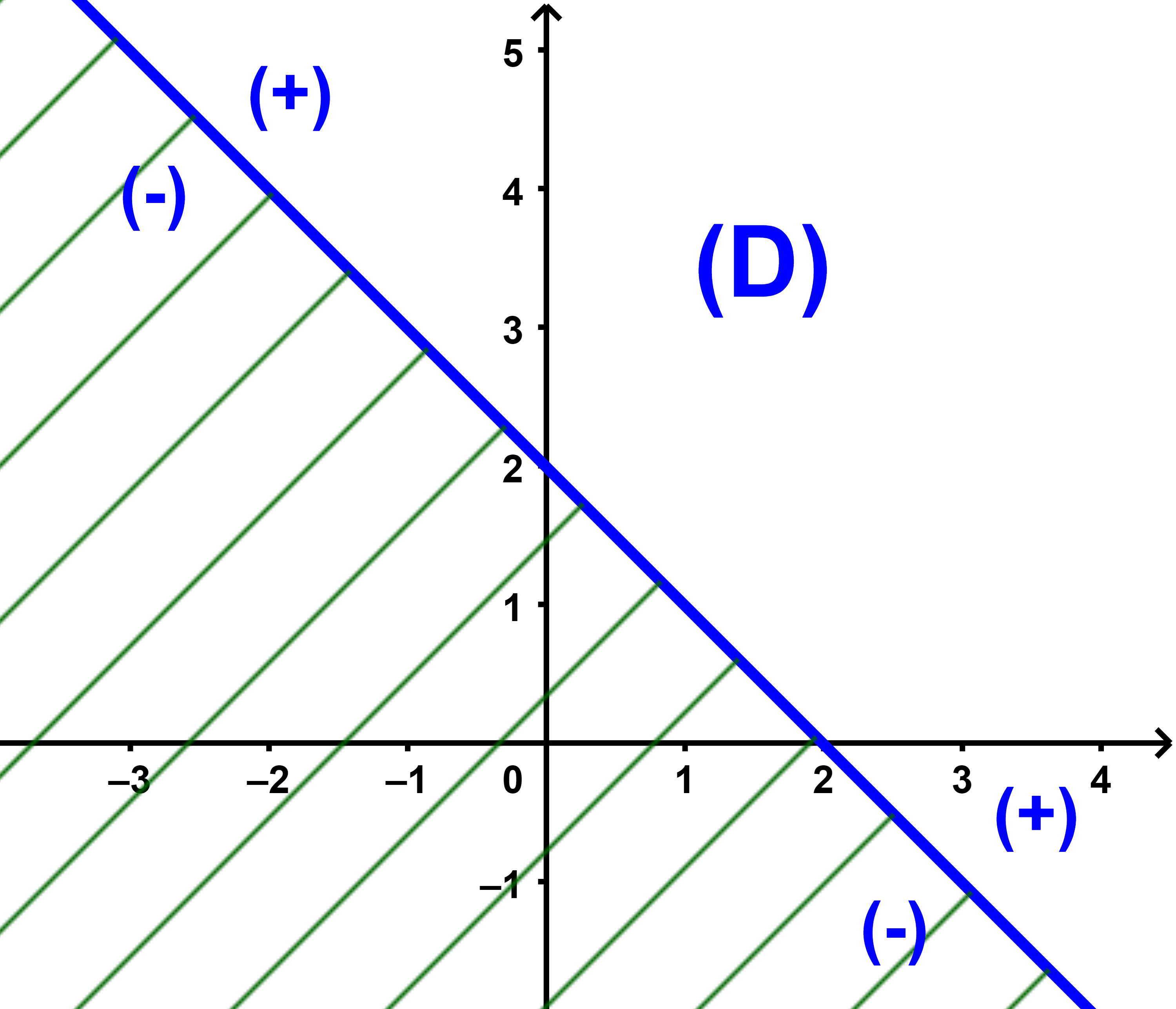
أولا ننشئ المستقيم (D) الذي معادلته x+y-2=0.
ثانيا نعتبر نقطة لا تنتمي الى المستقيم (D) لتكن O(0;0).

لدينا 0+0-2=-2<0 اذن نصف المستوى الذي حدوده (D) ويحتوي على النقطة O
معرف بالمتراجحة x+y-2<0.

ونصف المستوى الذي حدوده (D) ولا يحتوي على النقطة O معرف بالمتراجحة x+y-2>0.
(b) مجموعة حلول المتراجحة x+y-2<0 هي مجموعة ازواج احداثيات نقط نصف المستوى الذي حدوده (D) ويحتوي على النقطة O.

2) (a) اشارة x-y+2.
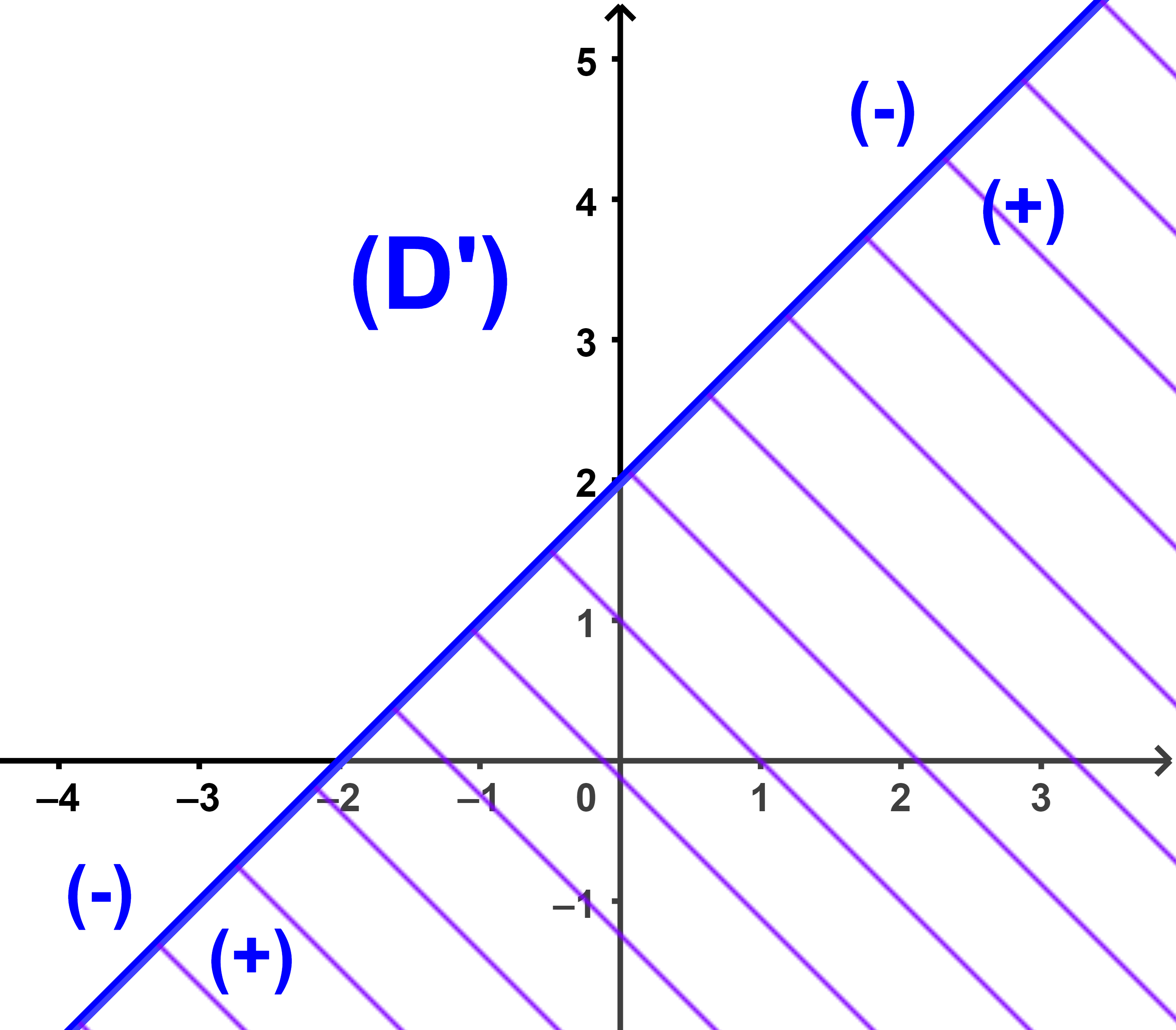
أولا ننشئ المستقيم (D') الذي معادلته x-y+2=0
ثانيا نعتبر نقطة لا تنتمي الى المستقيم (D'). لتكن O(0;0).
لدينا 0-0+2 = 2>0
اذن نصف المستوى الذي حدوده (D') ويحتوي على النقطة O
معرف بالمتراجحة x-y+2>0
ونصف المستوى الذي حدوده (D') ولا يحتوي على النقطة O
معرف بالمتراجحة x-y+2<0.

(b) مجموعة حلول المتراجحة x-y+2 < 0 هي مجموعة ازواج احداثيات نقط نصف المستوى الذي حدوده (D') ولا يحتوي على النقطة O.

3)
في هذا السؤال ينبغي انشاء المستقيميين
(D): x+y-2=0
و (D'): x-y+2=0 في نفس المعلم
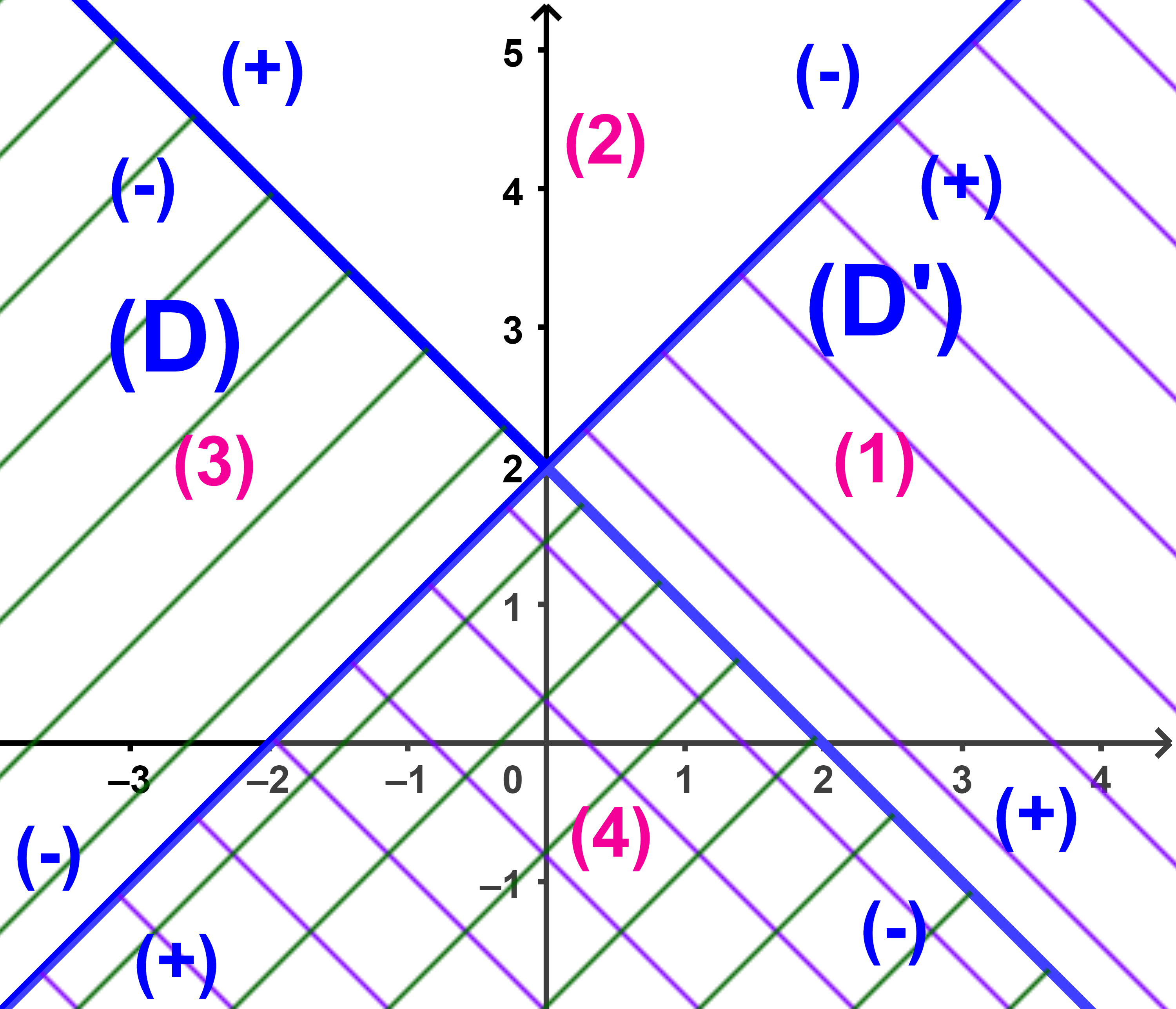
(a) (I): (x+y-2)(x-y+2)<0
تعني x+y-2 و x-y+2 لهما نفس الاشارة.
اذن مجموعة حلول المتراجحة (I) هي مجموعة ازواج احداثيات نقط الجزأين (1) و (3) من المستوى

(b) مجموعة حلول النظمة (S) هي مجموعة ازواج احداثيات نقط الجزأ (4) من المستوى