تمرين 1 tp

المستوى ℙ منسوب لمعلم متعامد ممنظم (O;i^→;j^→). نعتبر في ℙ نقطتين E(-3;2) و F(5;7).
حدد معادلة المستقيم (EF).

تصحيح

5-(-3)=8≠0 و 7-2=5≠0 اذن

x-(-3)	=	y-2
8		5

يعني 5(x+3)=8(y-2).

5x-8y+31=0 هي اذن معادلة ديكارتية للمستقيم (EF).

تمرين 2 tp

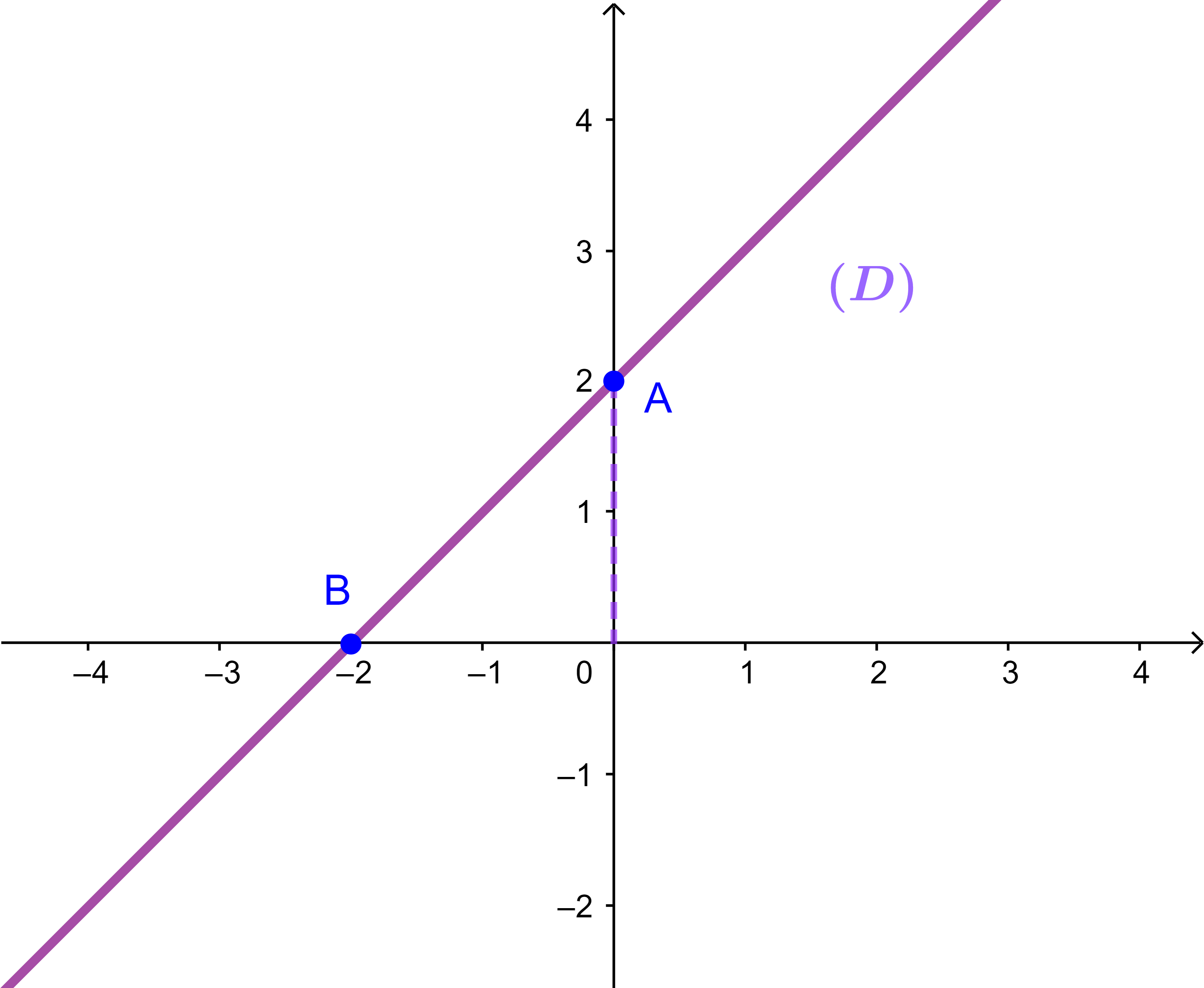
المستوى ℙ منسوب لمعلم متعامد ممنظم (O;i^→;j^→). نعتبر في ℙ المستقيم (AB) المعرف مبيانيا

حدد معادلة المستقيم (AB).

تمرين 3 tp

المستوى ℙ منسوب لمعلم متعامد ممنظم (O;i^→;j^→). نعتبر في ℙ مستقيما (D) معرفا كما يلي

x+5	=	y-3
4		7

حدد متجهة موجهة للمستقيم (D) ونقطة منه.

تمرين 4 tp

المستوى ℙ منسوب الى معلم متعامد ممنظم (O;i^→;j^→) .
لتكن E(4;0) و F(0;2) نقطتين من المستوى.
1) حدد معادلة ديكارتية للمستقيم (EF).
2) انشئ المستقيم (EF).

تمرين 5 tp

المستوى ℙ منسوب الى معلم متعامد ممنظم (O;i^→;j^→).
(D) مستقيم معادلته 2x+y-2=0.
1) حدد المعادلة المختصرة للمستقيم (D) واستنتج ميله.
2) انشئ المستقيم (D).