5- Résolution graphique des équations et inéquations

Exercice 1 tp

Soient f et g deux fonctions définies par:
f(x)=-2x²+4x+1 et g(x)=x²-4x+5
et (C_f) et (C_g) leurs courbes respectivement dans un repère orthonormé (O;i^→;j^→).
1) (a) Montrer que pour tout x∈IR
f(x)=-2(x-1)²+3.

(b) Déduire une valeur maximale de f.
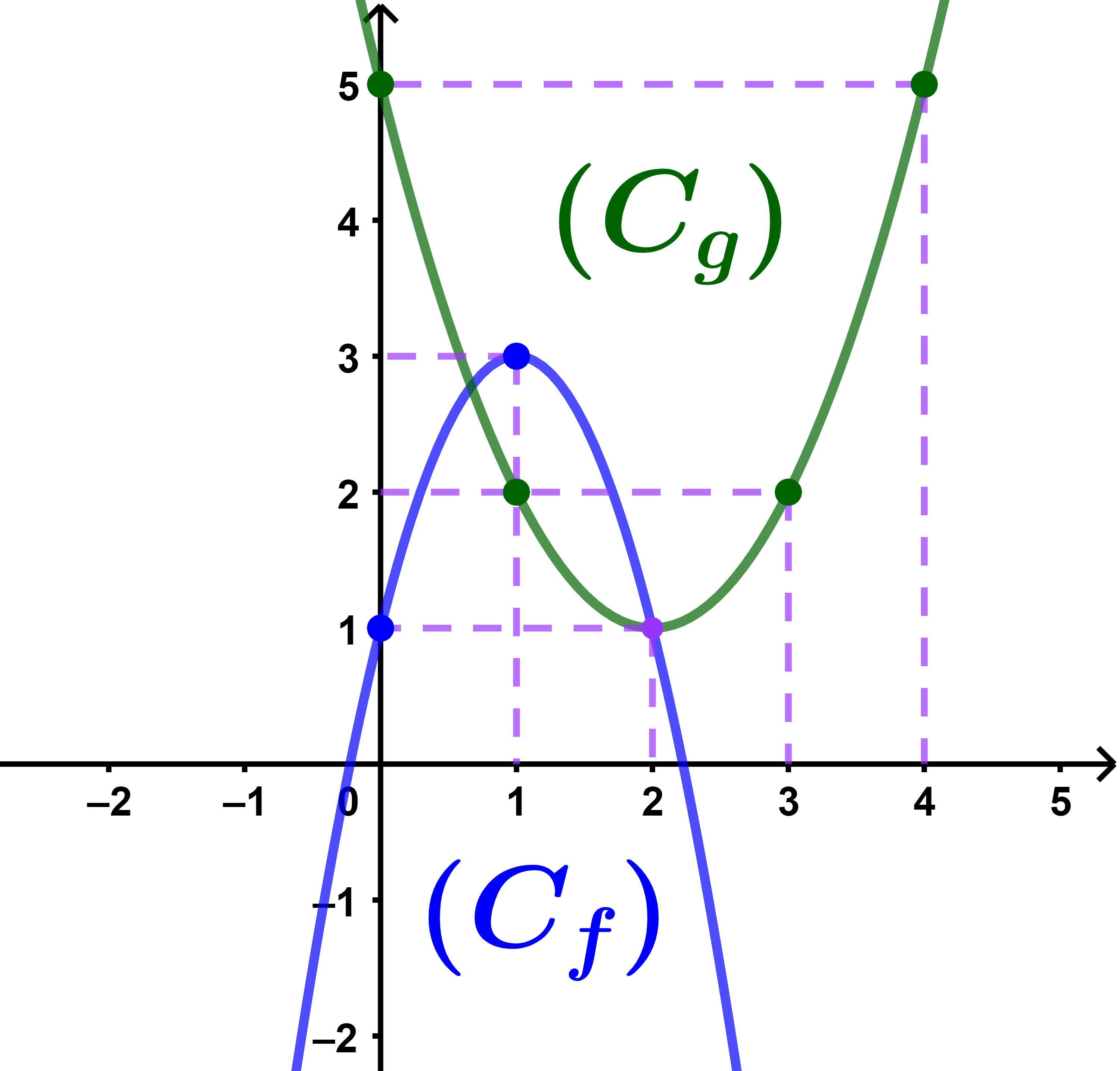
2) En utilisant la figure ci_jointe
(a) Résoudre graphiquement l'équation f(x)=g(x).
(b) Résoudre graphiquement l'inéquation f(x)≥g(x).

Exercice 2 tp

Soit f une fonction numérique de la variable réel x définie par
f(x)=x²-2x-1.
et (C) sa courbe représentative dans un repère orthonormé (O;i^→;j^→).
1) Montrer que pour tout x∈IR
on a f(x)=(x-1)²-2.
2) Calculer f(1) et montrer que
pour tout x∈IR on a f(x)-f(1)≥0.

3) Déduire un extremum de f.
4) (a) Calculer f(-1) ; f(2) ; f(3).
(b) Construire la courbe (C) et déduire les variations de f.
(c) Résoudre l'équation f(x)=m selon les valeurs de m.

Exercice 3 tp

Soit f une fonction numérique de la variable réel x définie par
f(x)=-2x²-4x+3.
et (C) sa courbe représentative dans un repère orthonormé (O;i^→;j^→).
1) Montrer que pour tout x∈IR
on a f(x)=-2(x + 1)²+5.
2) Calculer f(-1) et montrer que
pour tout x∈IR on a f(x)-f(-1)≤0.

3) Déduire un extremum de f.
4) (a) Calculer f(-2) ; f(0) ; f(1).
(b) Construire la courbe (C) et déduire les variations de f.
(c) Résoudre l'équation f(x)=m selon les valeurs de m.