2.2.4 المجال المركزي

تعريف
ليكن I مجالا (أو حيز ).
نقول ان I مجال مركزي في 0 او مماثل بالنسبة للصفر اذا تحقق الشرط التالي
اذا كان x∈I فان (-x)∈I.

أمثلة
1) I=[-4;4] مجال مركزي مركزه 0.
2) J=]-5;5] ليس مجالا مركزيا في 0 لان 5∈J ولكن (-5) ∉J.
3) D=]-4;-2]∪[2;4[ حيز مركزي مركزه 0 قلنا حيز لانه اتحاد مجالين وليس مجالا واحدا.

2.2.5 مركز وشعاع مجال محدود

تعريف
ليكن I مجالا محدودا طرفاه a و b حيث a<b.
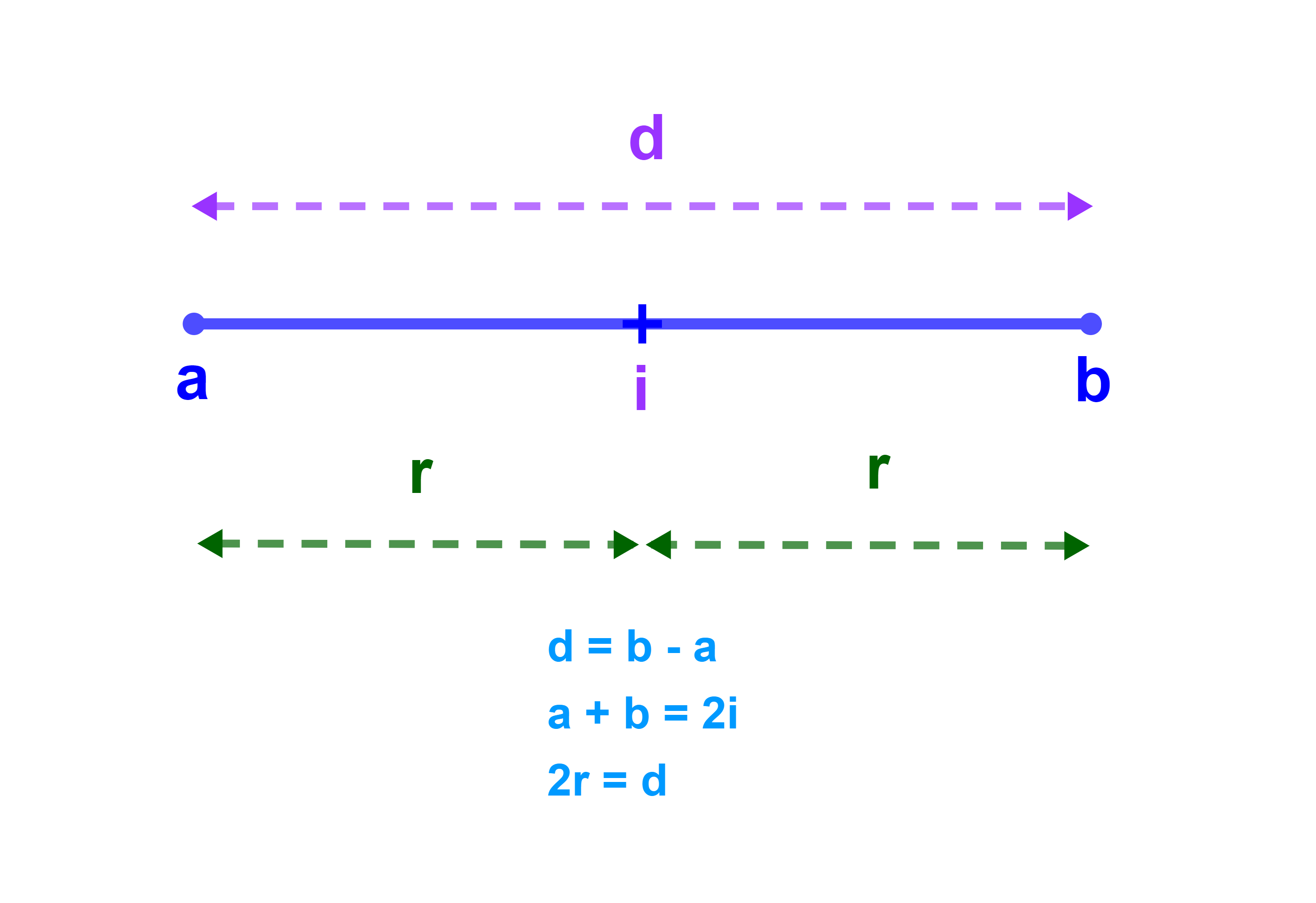
نقول ان α مركز المجال I اذاكان α-a=b-α=r والعدد r يسمى شعاع المجال I.
وتعبير آخر α مركز I اذا كان a+b=2α.
للتذكير العدد r=α-a=b-α شعاع المجال I.

نتيجة ليكن I مجالا مركزه α وشعاعه r .

α =	a+b	و	r =	b-a
	2			2

تمرين 1 tp

1) ليكن I=[2;12] مجالا.
حدد مركز وشعاع I.

تصحيح

1) نرمز ب i لمركز المجال I وب r لشعاعه

i =	2+12	= 7
	2
r =	12-2	= 5
	2

اذن I مجالا مركزه 7 وشعاعه 5.

تمرين 2 tp

حدد جميع المجالات التي مركزها 3 وشعاعها 1.

تصحيح

لكن I مجالا مركزه 3 وشعاعه 1.
اذن طرفاه هما 1+3=4 و 3-1=2.

المجالات اذن التي مركزها 3 وشعاعها 1 هي

[2 ; 4]		]2 ; 4[
[2 ; 4[		]2 ; 4]