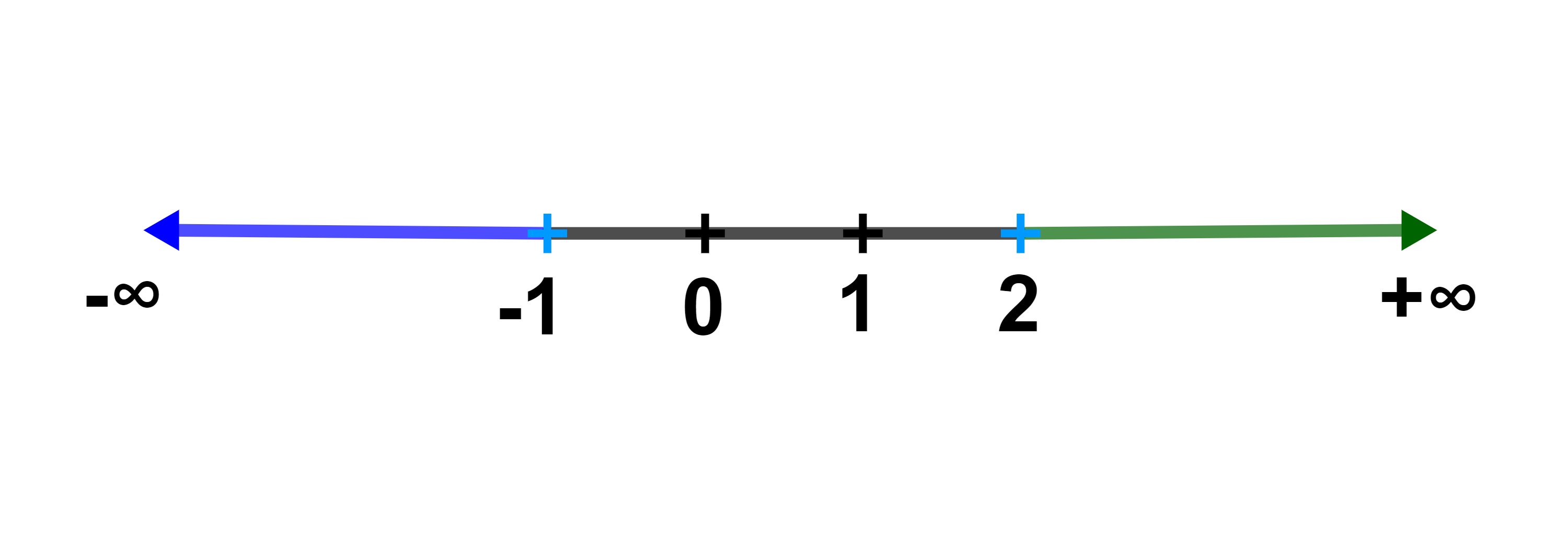تمرين 1 tp

1) ليكن x∈IR.
الى اي مجال ينتمي x
بحيث 2x+3≤7 ?
2) ليكن x∈IR.
الى أي مجال ينتمي x
بحيث -3x+4≥13 ?

تصحيح

1) ليكن x∈IR.
2x+3≤7 يعني 2x≤7-3
يعني 2x≤4 يعني x≤2
اذن x∈]-∞;2].
-∞ --- 2 --- → +∞

2) ليكن x∈IR.
-3x+4≥12 يعني -3x≥13-4
يعني -3x≥9 يعني 3x≤-9
يعني x≤-3 وبالتالي x∈]-∞;-3] .
-∞ --- -3 --- → +∞.

تمرين 2 tp

نعتبر المجموعة التي نرمز لها ب D والمكونة من الأعداد الحقيقية باستثناء العدد 1.
اكتب المجموعة D على شكل مجال او اتحاد مجالات.

تصحيح

لدينا D=IR\{1}.
x∈D يعني x≠1
يعني (x>1 أو x<1).
x>1 يعني x∈I=]1;+∞[.
x<1 يعني x∈J=]-∞;1[.

لدينا اذن
x∈D يعني x ينتمي الى اتحاد المجالين I و J
وبالتالي D=]-∞;1[∪]1;+∞[.

تمرين 4 tp

نعتبر المجموعة التي نرمز لها ب D والمكونة من الأعداد الحقيقية باستثناء العددين -1 و 2
اكتب المجموعة D على شكل مجال او اتحاد مجالات.

تصحيح

D=IR\{-1;2}.
x∈D يعني (x≠-1) و (x≠2).
النقطتان اللتان أفصولهما على التوالي (-1) و 2 على المستقيم العددي يحددان 3 أجزاء من المحور.

لدينا اذن
x∈D يعني (x<-1) أو (-1<x<2) أو (x>2).

لدينا x<-1 يعني x∈I=]-∞;-1[
-1<x<2 يعني x∈J=]-1;2[.
x>2 يعني x∈K=]2;+∞[
اذن x∈D يعني x ينتمي الى اتحاد المجالات I و J و K
وبالتالي D=]-∞;-1[∪]-1;2[∪]2;+∞[.