1- Repère dans le plan et Coordonnées

1.1 Repère dans le plan

1.1.1 Définition

Soient (OI) et (OJ) deux axes gradués sécants en O dans le plan.
Le triplet (O;OI^→;OJ^→) est appelé repère.

1.1.2 Repère orthonormé

Repère orthogonal
Si (O;OI^→;OJ^→) est un repère et (OI)⊥(OJ) alors le repère est orthogonal.

Repère orthonormé
Si (O;OI^→;OJ^→) est un repère orthogonal et OI=OJ alors le repère est orthonormé.

Remarque
Désormais le plan est rapporté au repère orthonormé (O;i^→;j^→).

1.2 Coordonnées d'un point et d'un vecteur

1.2.1 Introduction

Soient (OI) et (OJ) deux axes gradués sécants en O.
1) Soit M un point du plan. La droite parallèle à l'axe (OJ) et passant par M coupe l'axe (OI) au point H.
et la droite parallèle à l'axe (OI) et passant par M coupe l'axe (OJ) au point K.

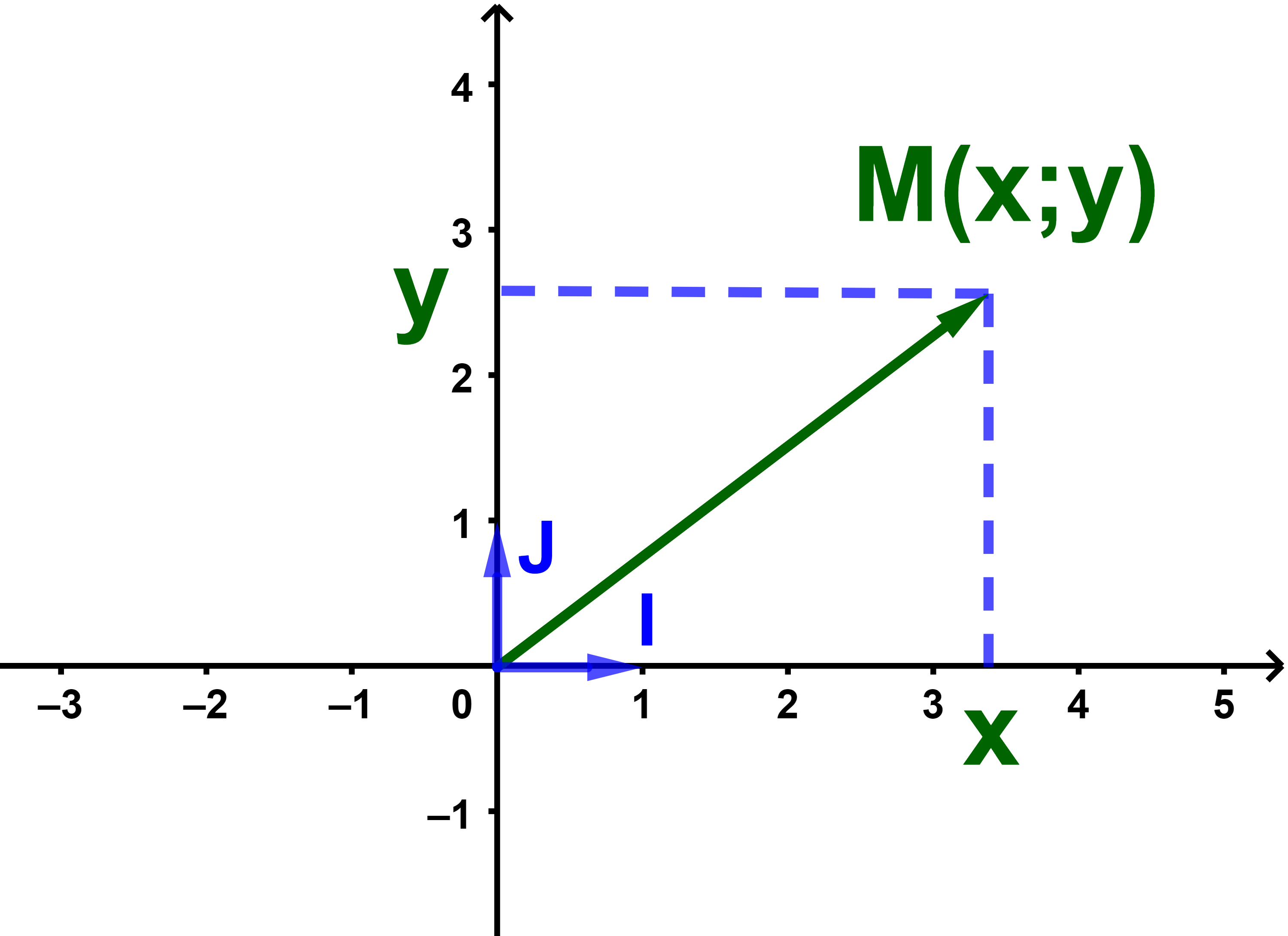
Si x est l'abscisse de H dans l'axe (OI)
et y est l'abscisse de K dans l'axe (OJ)
alors x et y sont appelés les coordonnées du point M et on écrit M(x;y).

x est l'abscisse de M et y est l'ordonnée de M.
2) x et y sont également les coordonnées du vecteur OM^→
et on écrit OM^→(x;y).

1.2.2 Propriété

Le plan est rapporté au repère orthonormé (O;i^→;j^→).
1) Si M est un point du plan alors il existe un couple (x;y) tel que OM^→=xi^→+yj^→ et on écrit M(x;y).
2) Si u^→ est un vecteur du plan alors il existe un couple (x;y) tel que u^→=xi^→+yj^→ et on écrit u^→(x;y).

Exercice 1 tp

Déterminer graphiquement les coordonnées des points A; B; C; D et E.

Exercice 2 tp

Construire dans un repère orthonormé les points A(-2;0) ; B(1;3) ; C(0;4) ; E(-3;-2).

Remarques
1) Le point F(a;b) appartient à l'axe des abscisses (Ox) si et seulement si b=0.
2) Le point F(a;b) appartient à l'axe des ordonnées (Oy) si et seulement si a=0.
3) a=b=0 signifie que F=O origine du repère.

Exemple O(0;0) est l'origine du repère.