3- التناسبية

3.1 التناسبية المباشرة

3.1.1 مثال

لدينا

24	= 3		12	= 3
8			4

اذن

24	=	12	= 3
8		4

نقول ان الأعداد 24 و 8 و 12 و 4 متناسبة
وأيضا 24 و 12 متناسبان مع 8 و 4.

3.1.2 تعريف

نقول ان الأعداد غير المنعدمة a و b و c و d في هذا الترتيب متناسبة اذا

ad=bc أو	a	=	c
	b		d

أمثلة
1) 15 و 20 و 7,5 و 10 متناسبة لان 15.10=20.7,5 (150=150)
2) 24 و 8 و 30 و 10 متناسبة لان 24.10=8.30 (240=240)

3.2 التناسب

3.2.1 تعريف

نقول ان الأعداد غير المنعدمة a و b و c و d في هذا الترتيب متناسبة عكسيا اذا

a	=	c
1		1
b		d
ab = cd أو

3.2.2 أمثلة

1) 3 و 15 و 9 و5 متناسبة عكسيا لأن 3.15=9.5
2) 10 و 7و 5 و 14 متناسبة عكسيا لأن 10.7=5.14

ملاحظة
معادلة مستقيم مار من أصل المعلم ومعاملة الموجه m تكتب على الشكل y=mx.

ماذا يمكن القول عن أراتيب النقط M(a;b) و N(c;d) لمستقيم (D) مار من أصل المعلم ((D): y=ax) ?

مثال ليكن (D): y=2x مستقيما.

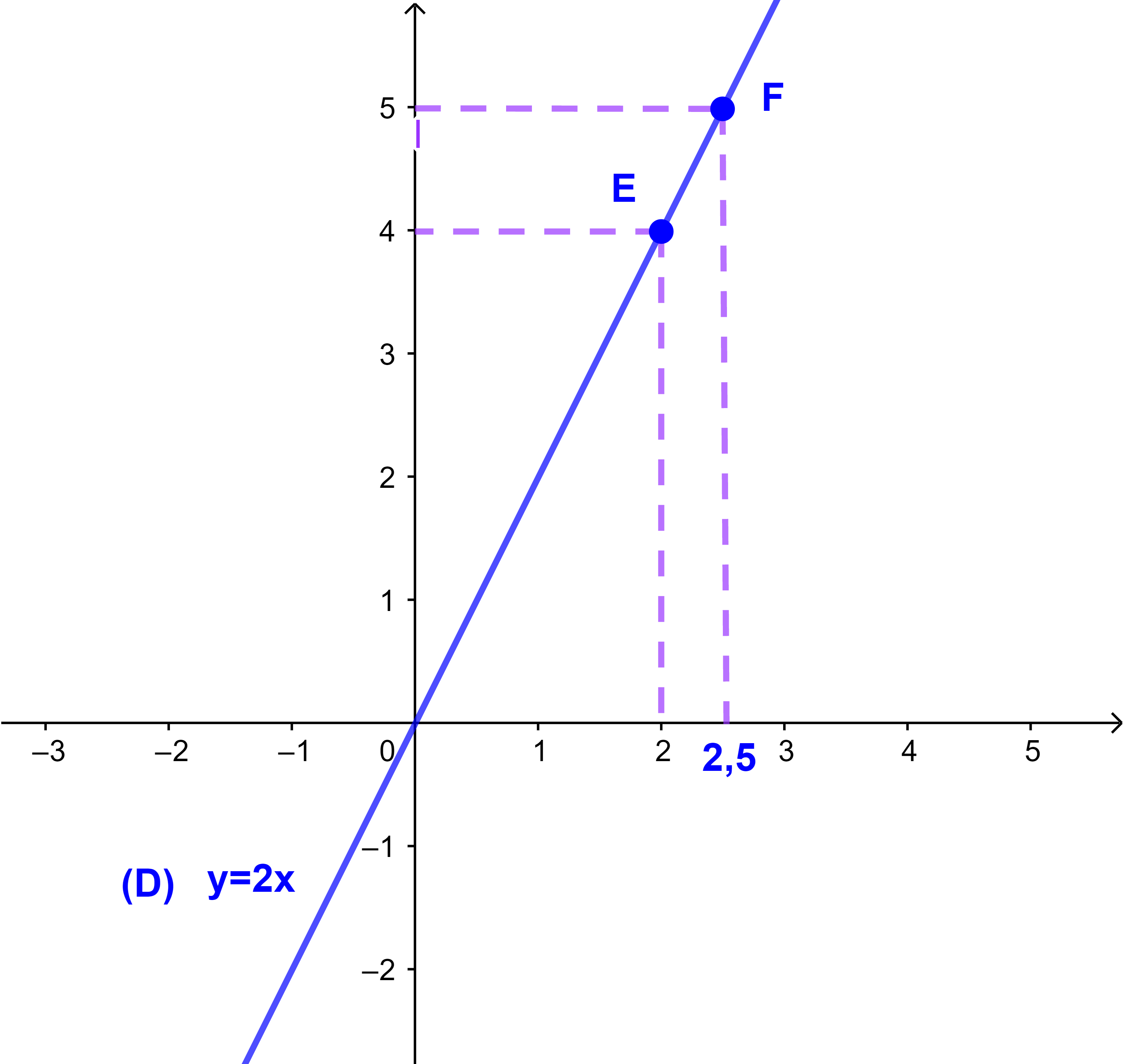
نتحقق أن E(2;4) و F(2,5;5) تنتمي (D).
بما أن 2.5=4.(2,5)=10 فان 4 و 5 متناسبة مع 2 و 2,5.

نتيجة
أراتيب نقط مستقيم مار من اصل المعلم متناسبة مع الافاصيل.

اذا كانت A(a;b) و B(c;d) نقطتين من المستقيم الذي معادلته y=mx فان

b	=	d
a		c

مثال ليكن (D): y=4x مستقيما و E(3;12) و F(2;8) نقطتين من (D).
اذن 12 و 8 متناسبين مع 3 و 2.

12	=	8
3		2