المعادلات والمتراجحات والنظمات (1)
1- المعادلات والمتراجحات من الرتبة الأولى بمجهول واحد
عندما يرن هاتفك قبل ان تنظر الى الشاشة لا تعرف من المتصل.
لديك اذن معادلة ذات مجهول واحد وتريد حلها :)
1.1 المعادلات من الرتبة 1 بمجهول واحد
1.1.1 أنشطة وتذكير
في رصيد امين 100 درهم اشترى تذكرتين واحدة له والاخرى لصديقه من أجل حضور مشاهدة مقابلة كرة القدم وبقي له 30 درهم.
ما هو ثمن التذكرة الواحدة ?
تصحيح
نعين ب
x ثمن التذكرة اذن المسألة تؤول الى المعادلة التالية
2x+30=100
اي
2x+30+(-30)=100+(-30)
اي
2x=70
اي
x=35
ومنه فان ثمن التذكرة هو 35 درهم.
1.1.2 تعريف
المعادلة من الرتبة 1 بمجهول واحد تكتب على الشكل ax+b=0 حيث x مجهول و a و b ثابتان.
1.1.3 حلول المعادلة ax+b=0
نرمز ب S لمجموعة حلول المعادلة ax+b=0.
| x1 = | -b | فان a≠0 اذا كانت (1 |
| a | ||
| S = { | -b | } ومنه فان |
| a |
2) اذا كان a=0 فان ax+b=0
يكافئ
0x+b=0.
اذا كان b=0 فان
0x=0
صحيح لكل عدد حقيقي
x
اذن
S=IR.
اذا كان b≠0 فان
0x+b=0 تعني
b=0
وهذا
مستحيل اذن
S=∅.
تمرين 1 tp
حل في IR المعادلة 4x+5=0.
تصحيح
ليكن x∈IR. 4x+5=0 يعني 4x=-5
| x = | -5 | يعني |
| 4 |
| S = { | -5 | } وبالتالي |
| 4 |
تمرين 2 tp
ليكن ABC مثلثا متساوي الساقين. احسب x.
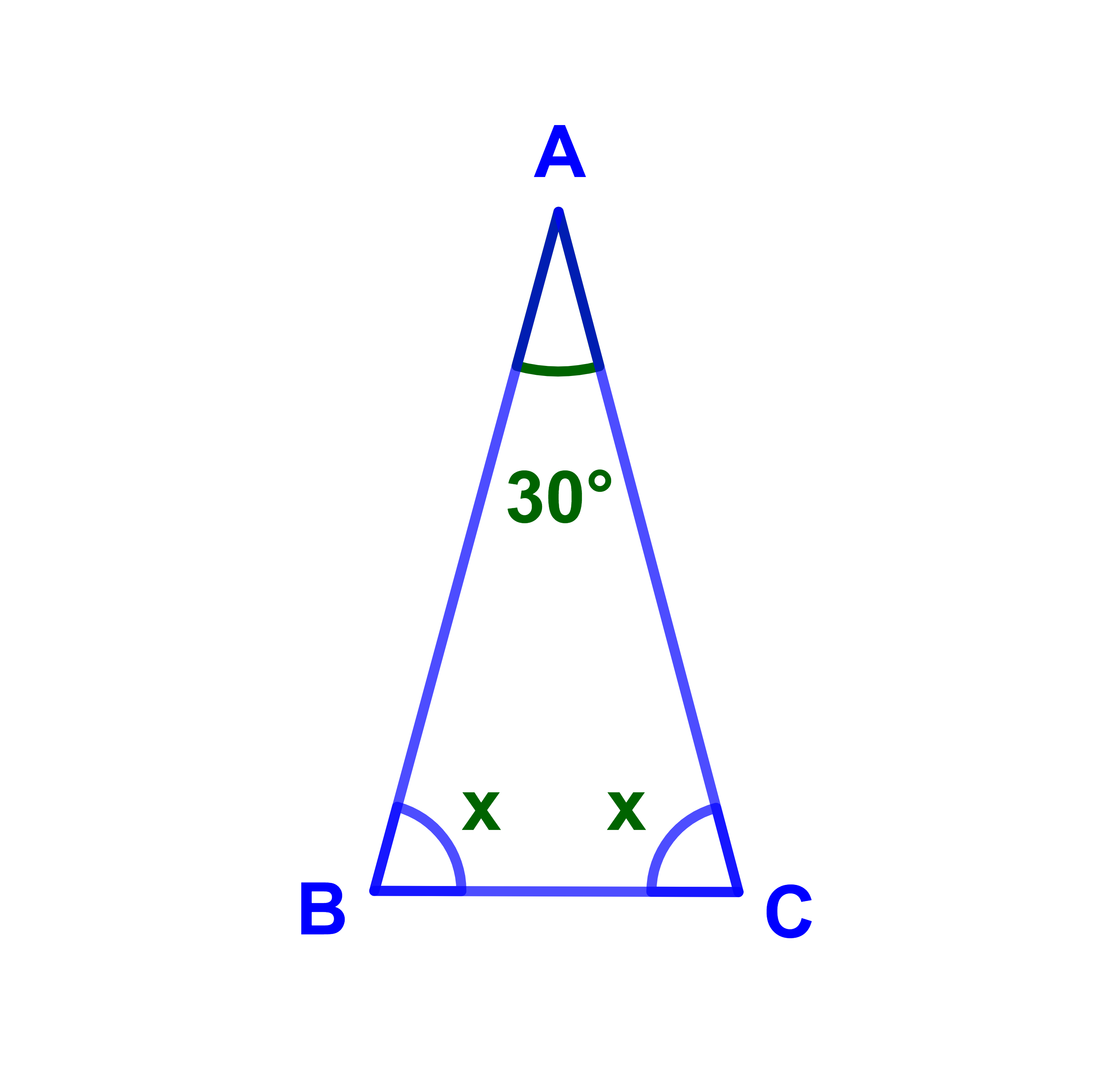
تمرين 3 tp
حل في IR المعادلة 3x-9=0.
تصحيح
ليكن x∈.
3x- 9=0 يعني
3x=+9
يعني
| x = | 9 | = 3 ∈IR |
| 3 |
وبالتالي مجموعة حلول المعادلة S={3}.
تمرين 4 tp
حل في IR المعادلة
3(x+5)-5(x+3)=0.
تصحيح
ليكن x∈IR.
3(x+5)-5(x+3)=0
يعني
3x+15-5x-15=0
يعني
3x-5x+15-15=0
يعني
(-2x)=0
(-2≠0) اذن x=0∈IR
وبالتالي مجموعة حلول المعادلة S={0}.