1- موضوعات التلاقي والأوضاع النسبية

1.1 موضوعات التلاقي في المستوى

1.1.1 موضوعة 1

نقطتان مختلفتان في الفضاء A و B تحددان مستقيما وحيدا في الفضاء.

تعريف
نقول ان ثلاث نفط أو اكثر مستقيمية اذا كانت تنتمي الى نفس المستقيم.

1.1.2 موضوعة 2

ثلاث نقط A و B و C غير مستقيمية في الفضاء تحدد مستوى وحيد نرمز له ب (ABC) أو P..

تعاريف
1) نقول ان أربع نقط او أكثر مستوائية في الفضاء اذا كانت تنتمي الى نفس المستوى.
2) نقول ان مستقيمين مستوائيان اذا كانا ضمن نفس المستوى.

1.1.3 موضوعة 3

اذا كانت A و B نقطتين من مستقيم تنتمي الى مستوى P فان هذا المستقيم ضمن المستوى (AB)⊂P.

1.1.4 موضوعة 4

اذا اشتركا مستويان مختلفان في نقطة فانهما متقاطعان وفق مستقيم مار من هذه النقطة.

ملاحظة
جميع خاصيات المستوى تبقى صحيحة في كل مستوى من الفضاء.

نتائج
1) مستقيمان متقاطعان يحددان مستوى وحيد.
2) نقطة A ومستقيم (D) لا يحتوي على A يحددان مستوى في القضاء.

1.2 الأوضاع النسبية في الفضاء

1.2.1 الأوضاع النسبية لمستقيم (D) ومستوى P

ليكن P مستوى و (D) مستقيما.
توجد ثلاث وضعيات
1) (D) يخترق المستوى P في نقطة واحدة A
(D)∩(P)={A}.
2) (D) ضمن المستوى P يعني(D)⊂P.
3) (D) و P منفصلان يعني(D)∩P=∅.

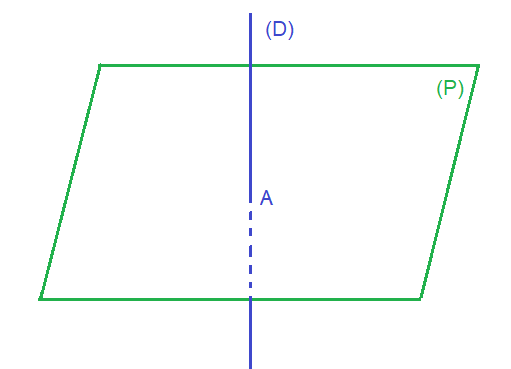
أمثلة
ليكن (ABCDEFGH) مكعبا
1) (AD)⊂(AEH) لان A∈(AD) و A∈(AEH).

بما ان AEHD مربع فان النقط A و E و H و D مستوائية
لدينا اذن A∈(AEH) و D∈(AEH) وبالتالي(AD)⊂(AEH).

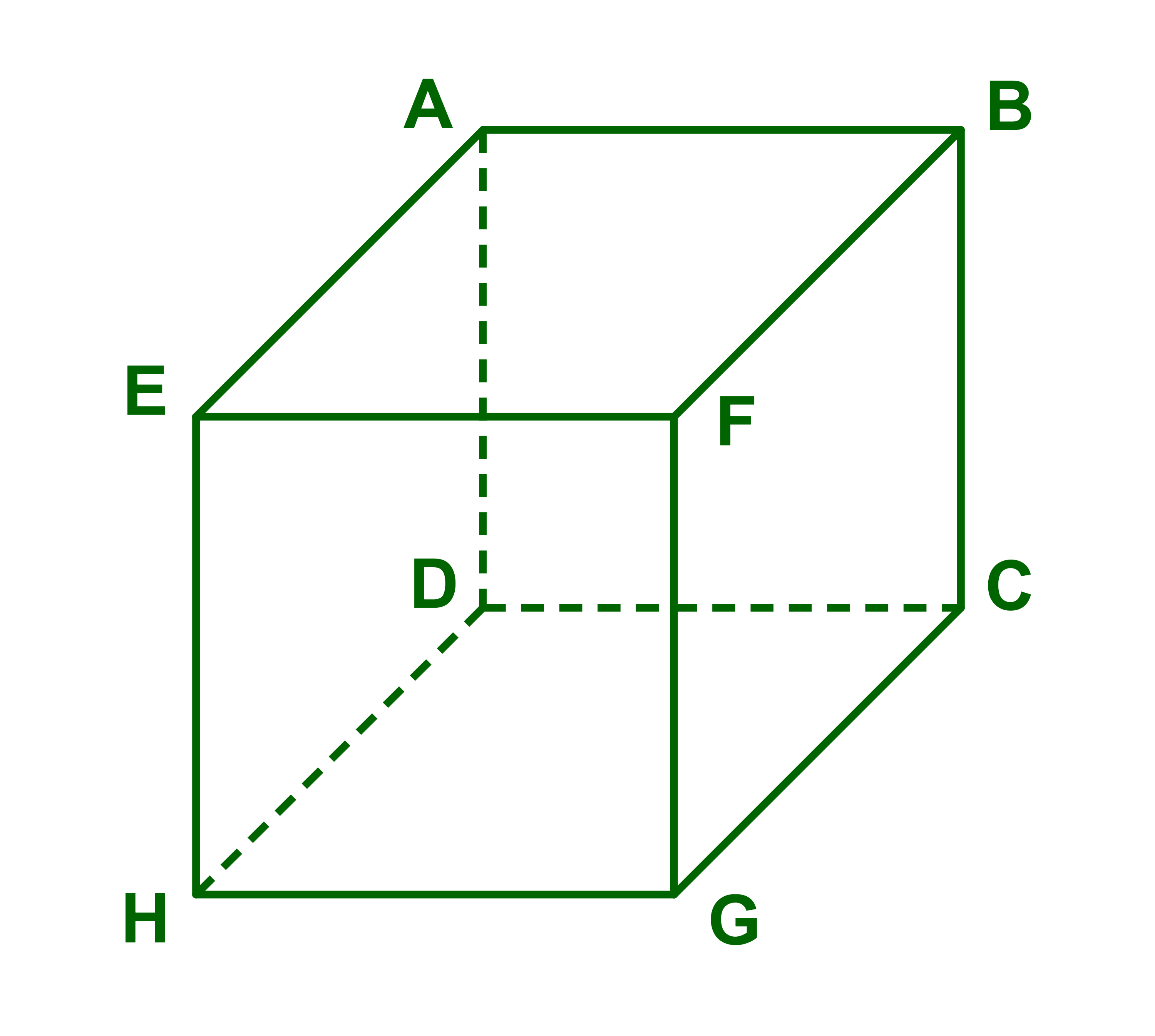
2) لدينا F∈(BCG) نفس برهان 1
اذن (HF) يخترق (BCG) نقطة واحدة F
والا (HF)⊂(BCG) ومنه فان H∈(BCG) وهذا مستحيل لان ABCDEFGH مكعب
وبالتالي (HF)∩(BCG)={F}.
3) (AE) و (DHG) منفصلان.
نفترض ان (AE) و (DHG) غير منفصلان
اذن (AE) يخترق المستوى (DHG)
ومنه فان (AE) يقطع المستقيم (HD) وهذا غير ممكن
وبالتالي (AE)∩(DHG)=∅.